Advertisements
Advertisements
प्रश्न
Find the ratio of the magnitude of the electric force to the gravitational force acting between two protons.
उत्तर
Charge of the proton, q = \[1 . 6 \times {10}^{- 19} C\]
Mass of the proton = \[1 . 67 \times {10}^{- 27} \text{ kg }\]
Let the distance between two protons be r.
Coulomb force (electric force) between the protons is given by
\[f_e = \frac{1}{4\pi \in_0} \times \frac{q^2}{r^2}\]
\[ = \frac{9 \times {10}^9 \times (1 . 6 )^2 \times {10}^{- 38}}{r^2}\]
Gravitational force between the protons is given by
\[f_g = \frac{\text{ G m}^2}{r^2}\]
\[ = \frac{6 . 67 \times {10}^{- 11} \times (1 . 67 \times {10}^{- 27} )^2}{r^2}\]
On dividing , \[f_e \text{ by } f_g\] , We get :
\[\frac{f_e}{f_g} = \frac{1}{4\pi \in_0} \times \frac{q^2}{r^2} \times \frac{r^2}{\text{ G m} ^2}\]
\[ = \frac{9 \times {10}^9 \times 1 . 6 \times 1 . 6 \times {10}^{- 38}}{6 . 67 \times {10}^{- 11} \times 1 . 67 \times 1 . 67 \times {10}^{- 54}}\]
\[ = \frac{9 \times (1 . 6 )^2 \times {10}^{- 29}}{6 . 67 \times (1 . 67 )^2 \times {10}^{- 65}}\]
\[ = 1 . 24 \times {10}^{36}\]
APPEARS IN
संबंधित प्रश्न
A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by
`F = -hati+2hatj+3hatkN`
Where `hati,hatj,hatk` are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
A lawyer alleges in court that the police had forced his client to issue a statement of confession. What kind of force is this ?
A neutron exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weak
Two spherical bodies, each of mass 50 kg, are placed at a separation of 20 cm. Equal charges are placed on the bodies and it is found that the force of Coulomb repulsion equals the gravitational attraction in magnitude. Find the magnitude of the charge placed on either body.
A monkey is sitting on a tree limb. The limb exerts a normal force of 48 N and a frictional force of 20 N. Find the magnitude of the total force exerted by the limb on the monkey.
The force with which the earth attracts an object is called the weight of the object. Calculate the weight of the moon from the following data : The universal constant of gravitation G = 6.67 × 11−11 N−m2/kg2, mass of the moon = 7.36 × 1022 kg, mass of the earth = 6 × 1024 kg and the distance between the earth and the moon = 3.8 × 105 km.
The magnetic force on a charged particle is always perpendicular to its velocity. Can the magnetic force change the velocity of the particles? Speed of the particle?
The work done by all the forces (external and internal) on a system equals the change in ______.
A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the plane. The motion of the particle takes place in a plane. It follows that
(a) its velocity is constant
(b) its acceleration is constant
(c) its kinetic energy is constant
(d) it moves in a circular path.
A box is pushed through 4.0 m across a floor offering 100 N resistance. How much work is done by the resisting force?
A block of mass 250 g slides down an incline of inclination 37° with uniform speed. Find the work done against friction as the block slides through 1m.
A box weighing 2000 N is to be slowly slid through 20 m on a straight track with friction coefficient 0⋅2 with the box. (a) Find the work done by the person pulling the box with a chain at an angle θ with the horizontal. (b) Find the work when the person has chosen a value of θ, which ensures him the minimum magnitude of the force.
A block of mass 2 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. Find the kinetic energy of the block at the instant the force ceases to act. Take g = 10 m/s2.
A 250 g block slides on a rough horizontal table. Find the work done by the frictional force in bringing the block to rest if it is initially moving at a speed of 40 cm/s. If the friction coefficient between the table and the block is 0⋅1, how far does the block move before coming to rest?
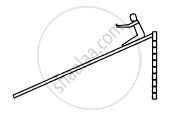
In a children's park, there is a slide which has a total length of 10 m and a height of 8⋅0 m . A vertical ladder is provided to reach the top. A boy weighing 200 N climbs up the ladder to the top of the slide and slides down to the ground. The average friction offered by the slide is three tenth of his weight. Find (a) the work done by the ladder on the boy as he goes up; (b) the work done by the slide on the boy as he comes down. Neglect any work done by forces inside the body of the boy
A particle of mass m is kept on a fixed, smooth sphere of radius R at a position where the radius through the particle makes an angle of 30° with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance travelled by the particle before it loses contact with the sphere.
A force F = 20 + 10y acts on a particle in y-direction where F is in newton and y in metre. Work done by this force to move the particle from y – 0 to y – 1 m is:
