Advertisements
Advertisements
प्रश्न
The force with which the earth attracts an object is called the weight of the object. Calculate the weight of the moon from the following data : The universal constant of gravitation G = 6.67 × 11−11 N−m2/kg2, mass of the moon = 7.36 × 1022 kg, mass of the earth = 6 × 1024 kg and the distance between the earth and the moon = 3.8 × 105 km.
उत्तर
The force between the Earth and the Moon is given by \[F = \frac{GMm}{r^2}\]
Here, M is the mass of the earth; m is the mass of the moon and r is the distance between Earth and Moon.
On substituting the values, we get :
\[F = \frac{6 . 67 \times {10}^{- 11} \times 7 . 36 \times {10}^{22} \times 6 \times {10}^{24}}{3 . 8 \times 3 . 8 \times {10}^{16}}\]
\[= \frac{6 . 67 \times 7 . 36 \times {10}^{35}}{(3 . 8 )^2 \times {10}^{16}}\]
\[ = 20 . 3 \times {10}^{19} = 2 . 03 \times {10}^{20} \]
\[ \approx 2 . 0 \times {10}^{20} N\]
∴ The weight of the moon is \[2 . 0 \times {10}^{20} N\]
APPEARS IN
संबंधित प्रश्न
State if the following statement is true or false. Give a reason for your answer.
Work done in the motion of a body over a closed loop is zero for every force in nature.
A body of mass m is placed on a table. The earth is pulling the body with a force mg. Taking this force to be the action what is the reaction?
List all the forces acting on the block B in figure.
When Neils Bohr shook hand with Werner Heisenberg, what kind of force they exerted ?
Let E, G and N represent the magnitudes of electromagnetic gravitational and nuclear forces between two electrons at a given separation. Then
A neutron exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weak
If all matters were made of electrically neutral particles such as neutrons,
(a) there would be no force of friction
(b) there would be no tension in the string
(c) it would not be possible to sit on a chair
(d) the earth could not move around the sun.
Which of the following systems may be adequately described by classical physics ?
(a) motion of a cricket ball
(b) motion of a dust particle
(c) a hydrogen atom
(d) a neutron changing to a proton.
The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10−17 N. Calculate the separation between the particles.
A satellite is projected vertically upwards from an earth station. At what height above the earth's surface will the force on the satellite due to the earth be reduced to half its value at the earth station? (Radius of the earth is 6400 km.)
Find the ratio of the magnitude of the electric force to the gravitational force acting between two protons.
A block of mass 5.0 kg slides down an incline of inclination 30° and length 10 m. Find the work done by the force of gravity.
A constant force of 2⋅5 N accelerates a stationary particle of mass 15 g through a displacement of 2⋅5 m. Find the work done and the average power delivered.
A force \[F = \alpha + bx\] acts on a particle in the x-direction, where a and b are constants. Find the work done by this force during a displacement from x = 0 to x = d.
A block of weight 100 N is slowly moved up a smooth incline of inclination 37° by a person. Calculate the work done by the person in moving the block through a distance of 2 m, if the driving force is (a) parallel to the incline and (b) in the horizontal direction.
A body is being raised to a height h from the surface of earth. What is the sign of work done by gravitational force?
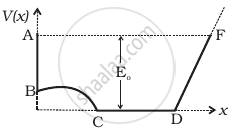
A graph of potential energy V(x) verses x is shown in figure. A particle of energy E0 is executing motion in it. Draw graph of velocity and kinetic energy versus x for one complete cycle AFA.
Force acting on a particle is (2`hat"i"` + 3 `hat"j"`) N. Work done by this force is zero, when a particle is moved on the line 3y + kx = 5. Here value of k is ______.
A body is displaced from (0, 0) to (1 m, 1 m) along the path x = y by a force F = (x2`hat"J"` + y`hat"i"`)N. The work done by this force will be:
