Advertisements
Advertisements
प्रश्न
Find the relation between x and y if the point M (x,y) is equidistant from R (0,9) and T (14 , 11).
उत्तर
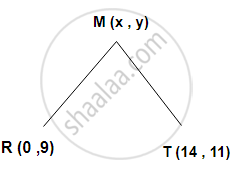
Given : MR = MT
∴ MR2 = MT2
(x - 0)2 + (y - 9)2 = (x - 14)2 + (y - 11)2
x2 + y2 + 81 - 18y = x2 + 196 - 28x + y2 + 121 - 22y
81 - 18y = 196 - 28x +121 - 22y
28 x - 18 y + 22 y = 196 + 121 - 81
28 x + 4y = 236
7x + y - 58 = 0
APPEARS IN
संबंधित प्रश्न
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b). Prove that bx = ay.
Show that the points (a, a), (–a, –a) and (– √3 a, √3 a) are the vertices of an equilateral triangle. Also find its area.
Find the coordinates of the centre of the circle passing through the points (0, 0), (–2, 1) and (–3, 2). Also, find its radius.
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (−3, 4).
Given A = (3, 1) and B = (0, y - 1). Find y if AB = 5.
The distance between the points (0, 5) and (–5, 0) is ______.
The distance between the point P(1, 4) and Q(4, 0) is ______.
Case Study -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie. Positions you might play include -
- Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K.
Using the picture of a hockey field below, answer the questions that follow:
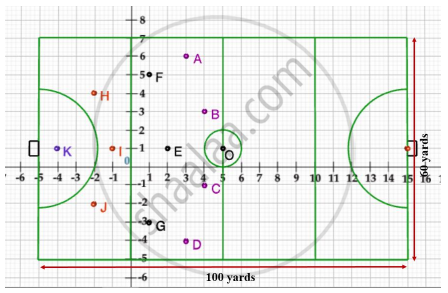
If a player P needs to be at equal distances from A and G, such that A, P and G are in straight line, then position of P will be given by ______.
Name the type of triangle formed by the points A(–5, 6), B(–4, –2) and C(7, 5).
The centre of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, – 9) and has diameter `10sqrt(2)` units.
