Advertisements
Advertisements
Question
Find the relation between x and y if the point M (x,y) is equidistant from R (0,9) and T (14 , 11).
Solution
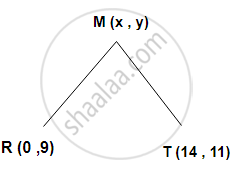
Given : MR = MT
∴ MR2 = MT2
(x - 0)2 + (y - 9)2 = (x - 14)2 + (y - 11)2
x2 + y2 + 81 - 18y = x2 + 196 - 28x + y2 + 121 - 22y
81 - 18y = 196 - 28x +121 - 22y
28 x - 18 y + 22 y = 196 + 121 - 81
28 x + 4y = 236
7x + y - 58 = 0
APPEARS IN
RELATED QUESTIONS
If A(5, 2), B(2, −2) and C(−2, t) are the vertices of a right angled triangle with ∠B = 90°, then find the value of t.
Show that four points (0, – 1), (6, 7), (–2, 3) and (8, 3) are the vertices of a rectangle. Also, find its area
An equilateral triangle has two vertices at the points (3, 4) and (−2, 3), find the coordinates of the third vertex.
Find the centre of the circle passing through (6, -6), (3, -7) and (3, 3)
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
Prove that the points (6 , -1) , (5 , 8) and (1 , 3) are the vertices of an isosceles triangle.
Prove that the points (0 , 2) , (1 , 1) , (4 , 4) and (3 , 5) are the vertices of a rectangle.
KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.
Find distance between point A(7, 5) and B(2, 5)
Show that the points (0, –1), (8, 3), (6, 7) and (– 2, 3) are vertices of a rectangle.
