Advertisements
Advertisements
प्रश्न
उत्तर
Common difference of the A.P. (d) = a2 - a1
\[= 15\frac{1}{2} - 18\]
\[ = \frac{31}{2} - 18\]
\[ = \frac{31 - 36}{2}\]
\[ = \frac{- 5}{2}\]
So here,
First term (a) = 18
Last term (l) = \[- 49\frac{1}{2} = \frac{- 99}{2}\]
Common difference (d) = \[\frac{- 5}{2}\]
So, here the first step is to find the total number of terms. Let us take the number of terms as n.
Now, as we know,
`a_n = a+(n-1)d`
So, for the last term,
\[\frac{- 99}{2} = 18 + \left( n - 1 \right)\frac{- 5}{2}\]
\[\frac{- 99}{2} = 18 + \left( \frac{- 5}{2} \right)n + \frac{5}{2}\]
\[\frac{5}{2}n = 18 + \frac{5}{2} + \frac{99}{2}\]
\[\frac{5}{2}n = 18 + \frac{104}{2}\]
\[n = 28\]
Now, using the formula for the sum of n terms, we get
\[S_n = \frac{28}{2}\left[ 2 \times 18 + \left( 28 - 1 \right)\left( \frac{- 5}{2} \right) \right]\]
\[ S_n = 14\left[ 36 + 27\left( \frac{- 5}{2} \right) \right]\]
\[ S_n = - 441\]
Therefore, the sum of the A.P is \[S_n = - 441\]
APPEARS IN
संबंधित प्रश्न
The sum of n, 2n, 3n terms of an A.P. are S1 , S2 , S3 respectively. Prove that S3 = 3(S2 – S1 )
A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A of radii 0.5, 1.0 cm, 1.5 cm, 2.0 cm, .... as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take `pi = 22/7`)

[Hint: Length of successive semicircles is l1, l2, l3, l4, ... with centres at A, B, A, B, ... respectively.]
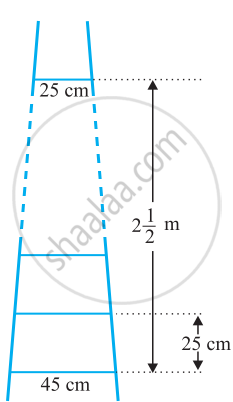
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
The sum of three terms of an A.P. is 21 and the product of the first and the third terms exceed the second term by 6, find three terms.
Find the value of x for which (x + 2), 2x, ()2x + 3) are three consecutive terms of an AP.
The first three terms of an AP are respectively (3y – 1), (3y + 5) and (5y + 1), find the value of y .
If the sum of first n terms is (3n2 + 5n), find its common difference.
How many terms of the AP 21, 18, 15, … must be added to get the sum 0?
Find out the sum of all natural numbers between 1 and 145 which are divisible by 4.
Q.17
