Advertisements
Advertisements
प्रश्न
Find the coordinates of circumcentre and radius of circumcircle of ∆ABC if A(7, 1), B(3, 5) and C(2, 0) are given.
उत्तर
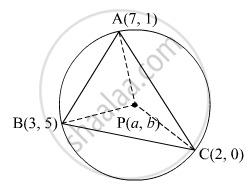
Let the circumcentre be P(a, b).
The given points are A(7, 1), B(3, 5) and C(2, 0).
The circumcircle passes through the points A, B and C and the thus,
PA = PB = PC
⇒ PA2 = PB2 = PC2
PA2 = PB2
⇒ (3 - a)2 + (5 - b)2 = (7 - a)2 + (1 - b)2
⇒ 9 + a2 - 6a + 25 + b2 - 10b = 49 + a2 - 14a + 1 + b2 - 2b
⇒ a - b = 2 ...(1)
PA2 = PC2
⇒ (7 - a)2 + (1 - b)2 = (2 - a)2 + (0 - b)2
⇒ 49 + a2 - 14a + 1 + b2 - 2b = 4 + a2 - 4a + b2
⇒ 5a + b = 23 ...(2)
(1) + (2)
`a = 25/6, b = 13/6`
Radius = PC =
= `sqrt((25/6 - 2)^2 + (13/6 - 0)^2)`
= `sqrt((13/6)^2 + (13/6 )^2)`
= `13/6sqrt2`
संबंधित प्रश्न
Prove that the points (−2, 5), (0, 1) and (2, −3) are collinear.
The three vertices of a parallelogram are (3, 4) (3, 8) and (9, 8). Find the fourth vertex.
In Fig. 14.36, a right triangle BOA is given C is the mid-point of the hypotenuse AB. Show that it is equidistant from the vertices O, A and B.

We have a right angled triangle,`triangle BOA` right angled at O. Co-ordinates are B (0,2b); A (2a, 0) and C (0, 0).
If the point P (2,2) is equidistant from the points A ( -2,K ) and B( -2K , -3) , find k. Also, find the length of AP.
Show that the following points are the vertices of a square:
A (0,-2), B(3,1), C(0,4) and D(-3,1)
If (2, p) is the midpoint of the line segment joining the points A(6, -5) and B(-2,11) find the value of p.
In what ratio does the point P(2,5) divide the join of A (8,2) and B(-6, 9)?
If the points P (a,-11) , Q (5,b) ,R (2,15) and S (1,1). are the vertices of a parallelogram PQRS, find the values of a and b.
Find the coordinates of the centre of the circle passing through the points P(6, –6), Q(3, –7) and R (3, 3).
What is the area of the triangle formed by the points O (0, 0), A (6, 0) and B (0, 4)?
Write the coordinates of the point dividing line segment joining points (2, 3) and (3, 4) internally in the ratio 1 : 5.
If the area of the triangle formed by the points (x, 2x), (−2, 6) and (3, 1) is 5 square units , then x =
The ratio in which the x-axis divides the segment joining (3, 6) and (12, −3) is
If Points (1, 2) (−5, 6) and (a, −2) are collinear, then a =
If the centroid of the triangle formed by (7, x) (y, −6) and (9, 10) is at (6, 3), then (x, y) =
The coordinates of the fourth vertex of the rectangle formed by the points (0, 0), (2, 0), (0, 3) are
What is the nature of the line which includes the points (-5, 5), (6, 5), (-3, 5), (0, 5)?
The point R divides the line segment AB, where A(−4, 0) and B(0, 6) such that AR=34AB.">AR = `3/4`AB. Find the coordinates of R.
Abscissa of all the points on the x-axis is ______.
Ordinate of all points on the x-axis is ______.
