Advertisements
Advertisements
प्रश्न
Find the coordinates of circumcentre and radius of circumcircle of ∆ABC if A(7, 1), B(3, 5) and C(2, 0) are given.
उत्तर
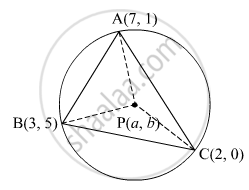
Let the circumcentre be P(a, b).
The given points are A(7, 1), B(3, 5) and C(2, 0).
The circumcircle passes through the points A, B and C and the thus,
PA = PB = PC
⇒ PA2 = PB2 = PC2
PA2 = PB2
⇒ (3 - a)2 + (5 - b)2 = (7 - a)2 + (1 - b)2
⇒ 9 + a2 - 6a + 25 + b2 - 10b = 49 + a2 - 14a + 1 + b2 - 2b
⇒ a - b = 2 ...(1)
PA2 = PC2
⇒ (7 - a)2 + (1 - b)2 = (2 - a)2 + (0 - b)2
⇒ 49 + a2 - 14a + 1 + b2 - 2b = 4 + a2 - 4a + b2
⇒ 5a + b = 23 ...(2)
(1) + (2)
`a = 25/6, b = 13/6`
Radius = PC =
= `sqrt((25/6 - 2)^2 + (13/6 - 0)^2)`
= `sqrt((13/6)^2 + (13/6 )^2)`
= `13/6sqrt2`
संबंधित प्रश्न
The base PQ of two equilateral triangles PQR and PQR' with side 2a lies along y-axis such that the mid-point of PQ is at the origin. Find the coordinates of the vertices R and R' of the triangles.
The three vertices of a parallelogram are (3, 4) (3, 8) and (9, 8). Find the fourth vertex.
Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1), (1, 0), (4, 3) and(1, 2) meet
Find the ratio in which the point (2, y) divides the line segment joining the points A (-2,2) and B (3, 7). Also, find the value of y.
In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
Prove that the points A(-4,-1), B(-2, 4), C(4, 0) and D(2, 3) are the vertices of a rectangle.
Determine the ratio in which the point P (m, 6) divides the join of A(-4, 3) and B(2, 8). Also, find the value of m.
Show that the following points are the vertices of a square:
(i) A (3,2), B(0,5), C(-3,2) and D(0,-1)
Points P, Q, and R in that order are dividing line segment joining A (1,6) and B(5, -2) in four equal parts. Find the coordinates of P, Q and R.
If the points A (2,3), B (4,k ) and C (6,-3) are collinear, find the value of k.
ΔXYZ ∼ ΔPYR; In ΔXYZ, ∠Y = 60o, XY = 4.5 cm, YZ = 5.1 cm and XYPY =` 4/7` Construct ΔXYZ and ΔPYR.
The points \[A \left( x_1 , y_1 \right) , B\left( x_2 , y_2 \right) , C\left( x_3 , y_3 \right)\] are the vertices of ΔABC .
(i) The median from A meets BC at D . Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the points of coordinates Q and R on medians BE and CF respectively such thatBQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What are the coordinates of the centropid of the triangle ABC ?
If the distance between points (x, 0) and (0, 3) is 5, what are the values of x?
Find the values of x for which the distance between the point P(2, −3), and Q (x, 5) is 10.
The distance between the points (cos θ, 0) and (sin θ − cos θ) is
If (x , 2), (−3, −4) and (7, −5) are collinear, then x =
Find the point on the y-axis which is equidistant from the points (5, −2) and (−3, 2).
If the sum of X-coordinates of the vertices of a triangle is 12 and the sum of Y-coordinates is 9, then the coordinates of centroid are ______
Students of a school are standing in rows and columns in their playground for a drill practice. A, B, C and D are the positions of four students as shown in figure. Is it possible to place Jaspal in the drill in such a way that he is equidistant from each of the four students A, B, C and D? If so, what should be his position?
In which ratio the y-axis divides the line segment joining the points (5, – 6) and (–1, – 4)?
