Advertisements
Advertisements
प्रश्न
The points \[A \left( x_1 , y_1 \right) , B\left( x_2 , y_2 \right) , C\left( x_3 , y_3 \right)\] are the vertices of ΔABC .
(i) The median from A meets BC at D . Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the points of coordinates Q and R on medians BE and CF respectively such thatBQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What are the coordinates of the centropid of the triangle ABC ?
उत्तर
(i) Median AD of the triangle will divide the side BC in two equal parts.
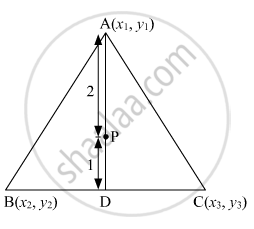
Therefore, D is the midpoint of side BC.
Coordinates of D are \[\left( \frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2} \right)\]
(ii)THe point P divided the side AD in the ratio 2: 1.
Coordinates of P are \[\left( \frac{2 \times \left( \frac{x_2 + x_3}{2} \right) + 1 \times x_1}{2 + 1}, \frac{2 \times \left( \frac{y_2 + y_3}{2} \right) + 1 \times y_1}{2 + 1} \right) = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)\]
(iii)
Median BE of the triangle will divide the side AC in two equal parts.
Therefore, E is the midpoint of side AC.
Coordinates of E are \[\left( \frac{x_1 + x_3}{2}, \frac{y_1 + y_3}{2} \right)\] The point Q divided the side BE in the ratio 2: 1.
Coordinates of Q are \[\left( \frac{2 \times \left( \frac{x_1 + x_3}{2} \right) + 1 \times x_2}{2 + 1}, \frac{2 \times \left( \frac{y_1 + y_3}{2} \right) + 1 \times y_2}{2 + 1} \right) = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)\]
Similarly, Coordinates of Q are R are \[\left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)\]
(iv)
The points P, Q and R coincides and is the centroid of the triangle ABC.
So, coordinates of the centroid is \[\left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)\]
APPEARS IN
संबंधित प्रश्न
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right-angled isosceles triangle.
On which axis do the following points lie?
R(−4,0)
If G be the centroid of a triangle ABC, prove that:
AB2 + BC2 + CA2 = 3 (GA2 + GB2 + GC2)
Show that the points A(5, 6), B(1, 5), C(2, 1) and D(6,2) are the vertices of a square.
Find a point on y-axis which is equidistant from the points (5, -2) and (-3, 2).
Prove that the points A(-4,-1), B(-2, 4), C(4, 0) and D(2, 3) are the vertices of a rectangle.
The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x - y + k = 0. Find the value of k.
Points A(-1, y) and B(5,7) lie on the circle with centre O(2, -3y).Find the value of y.
Show that `square` ABCD formed by the vertices A(-4,-7), B(-1,2), C(8,5) and D(5,-4) is a rhombus.
The abscissa of a point is positive in the
If the points P, Q(x, 7), R, S(6, y) in this order divide the line segment joining A(2, p) and B(7, 10) in 5 equal parts, find x, y and p.
ABCD is a parallelogram with vertices \[A ( x_1 , y_1 ), B \left( x_2 , y_2 \right), C ( x_3 , y_3 )\] . Find the coordinates of the fourth vertex D in terms of \[x_1 , x_2 , x_3 , y_1 , y_2 \text{ and } y_3\]
If the centroid of the triangle formed by points P (a, b), Q(b, c) and R (c, a) is at the origin, what is the value of a + b + c?
Find the values of x for which the distance between the point P(2, −3), and Q (x, 5) is 10.
What is the distance between the points \[A\left( \sin\theta - \cos\theta, 0 \right)\] and \[B\left( 0, \sin\theta + \cos\theta \right)\] ?
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k
If the centroid of the triangle formed by (7, x) (y, −6) and (9, 10) is at (6, 3), then (x, y) =
If the points(x, 4) lies on a circle whose centre is at the origin and radius is 5, then x =
The coordinates of a point on x-axis which lies on the perpendicular bisector of the line segment joining the points (7, 6) and (−3, 4) are
If A(x, 2), B(−3, −4) and C(7, −5) are collinear, then the value of x is
