Advertisements
Advertisements
प्रश्न
Find the graphical solution of the following system of linear inequations:
`"x"/60 + "y"/90 ≤ 1`, `"x"/120 + "y"/75 ≤ 1`, y ≥ 0, x ≥ 0
उत्तर
Consider the equations:
`"x"/60 + "y"/90 ≤ 1`
| x | 60 | 0 |
| y | 0 | 90 |
The two points on the axes are (60, 0) and (0, 90) as in equation 60 and 90 are x and y-intercepts,
(x and y are equivalent to X and Y axes.)
∵ The inequation `"x"/60 + "y"/90 ≤ 1` satisfies the origin.
The solution set is towards the origin.
`"x"/120 + "y"/75 ≤ 1`
| x | 120 | 0 |
| y | 0 | 75 |
The two points on the axes are (120, 0) and (0, 75) respectively.
The inequation `"x"/120 + "y"/75 ≤ 1` satisfies the origin.
The solution set of the inequation is towards origin x ≥ 0, y ≥0 are the inequations showing the conditions that the solutions set (common region) is in the first quadrant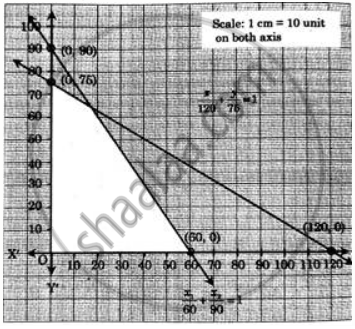
APPEARS IN
संबंधित प्रश्न
Solve the following system of inequalities graphically: 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically: x + y ≤ 6, x + y ≥ 4
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Find all pairs of consecutive even positive integers, both of which are larger than 5, such that their sum is less than 23.
A solution is to be kept between 30°C and 35°C. What is the range of temperature in degree Fahrenheit?
The longest side of a triangle is three times the shortest side and third side is 2 cm shorter than the longest side if the perimeter of the triangles at least 61 cm, find the minimum length of the shortest-side.
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If there are 640 litres of the 8% solution, how many litres of 2% solution will have to be added?
Write the number of integral solutions of \[\frac{x + 2}{x^2 + 1} > \frac{1}{2}\]
Find the graphical solution of the following system of linear inequations:
x – y ≤ 0, 2x – y ≥ − 2
Solve the following system of inequalities graphically.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
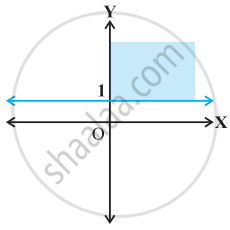
Find the linear inequalities for which the shaded region in the given figure is the solution set.
Solve the following system of inequalities `(2x + 1)/(7x - 1) > 5, (x + 7)/(x - 8) > 2`
Show that the following system of linear inequalities has no solution x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Show that the solution set of the following system of linear inequalities is an unbounded region 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0.
Solution set of x ≥ 0 and y ≤ 1 is