Advertisements
Advertisements
प्रश्न
Find the number of atoms in the fcc unit cell.
उत्तर
- A face-centred cubic (fcc) unit cell has particles at the eight corners plus particles at the centre of its six faces.
- Each particle present at the corner of a given unit cell is shared with seven other neighbouring unit cells. As a result, its contribution to the given unit cell is only `1/8`.
Thus, the number of particles present at corners per unit cell
= 8 corner atoms × `1/8` atom per unit cell = 1 - Each particle at the centre of the six faces is shared with one neighbouring cube. Thus, 1/2 of each face particle belongs to the given unit cell. Thus, the number of particles present at faces per unit cell
= 6 atoms at the faces × `1/2` atom per unit cell = 3
Therefore, fcc unit cell has one corner particle plus 3 face particles, making total of 4 particles per unit cell.
APPEARS IN
संबंधित प्रश्न
Obtain the relationship between the density of a substance and the edge length of the unit cell.
An element with molar mass 27 g/mol forms a cubic unit cell with edge length of 405 pm. If the density of the element is 2.7 g/cm3, what is the nature of the cubic unit cell?
Write the relationship between radius of atom and edge length of fcc unit cell.
The pyranose structure of glucose is ____________.
An element (atomic mass M g/mol) having bcc structure has unit cell edge 400 pm. The density of the element is ____________ g/cm3.
[NA = 6.0 × 1023 atom mol−1)
How many total constituent particles are present in simple cubic unit cell?
The number of atoms in 500 g of a fcc crystal of a metal with density d = 10 g/cm3 and cell edge 100 pm, is equal to ____________.
An element with density 2.8 g cm−3 forms fcc unit cell having edge length 4 × 10−8 cm. Calculate molar mass of the element.
Copper and silver have ____________ crystal structure.
Consider the following unit cell.
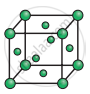
The number of particles (spheres) per unit cell is:
A metallic element has a cubic lattice with edge length of unit cell 2 Å. Calculate the number of unit cells in 200 g of the metal, if density of metal is 2.5 g cm-3?
What is the density of iron crystal which crystallizes in body-centred cubic structure with edge length 287 pm? (At. mass of Fe = 56 amu)
The coordination number of atoms in body-centred cubic structure (bcc) is ______.
Gold crystallises into face-centred cubic cells. The edge length of a unit cell is 4.08 × 10–8 cm. Calculate the density of gold. [Molar mass of gold = 197 g mol–1]
An element has a bee structure with unit cell edge length of 288 pm. How many unit cells and number of atoms are present in 200 g of the element?
In face centred cubic unit cell, what is the volume occupied?
Identify unit cell from following having four particles in it
At room temperature, polonium Crystallises in a primitive cubic unit cell. If a = 3.36 Å. Calculate the theoretical density of polonium. [It's atomic weight is 209 g/mol.]
Silver crystallizes in the fcc structure. If the edge length of the unit cell is 400 pm, calculate the density of silver (Atomic mass of Ag = 108).
The correct sequence of the atomic layers in cubic close packing is ______.
The total number of different primitive unit cells is ______.
What would be the empirical formula of a compound having a unit cell containing A ion shared equally at the corner of the cube and B ion on the centre of faces of the cube?
