Advertisements
Advertisements
Question
Find the number of atoms in the fcc unit cell.
Solution
- A face-centred cubic (fcc) unit cell has particles at the eight corners plus particles at the centre of its six faces.
- Each particle present at the corner of a given unit cell is shared with seven other neighbouring unit cells. As a result, its contribution to the given unit cell is only `1/8`.
Thus, the number of particles present at corners per unit cell
= 8 corner atoms × `1/8` atom per unit cell = 1 - Each particle at the centre of the six faces is shared with one neighbouring cube. Thus, 1/2 of each face particle belongs to the given unit cell. Thus, the number of particles present at faces per unit cell
= 6 atoms at the faces × `1/2` atom per unit cell = 3
Therefore, fcc unit cell has one corner particle plus 3 face particles, making total of 4 particles per unit cell.
APPEARS IN
RELATED QUESTIONS
Answer the following in brief.
Calculate the number of atoms in fcc unit cell.
Write the relationship between radius of atom and edge length of fcc unit cell.
Give the percentage of empty space in bcc lattice.
If the total volume of a simple cubic unit cell is 6.817 × 10-23 cm3, what is the volume occupied by particles in the unit cell?
Calculate the number of unit cells in 0.3 g of a species having density of 8.5 g/cm3 and unit cell edge length 3.25 × 10-8 cm.
Silver crystallises in fcc structure, if edge length of unit cell is 316.5 pm. What is the radius of silver atom?
What is the percentage of unoccupied space in fcc unit cell?
How many total constituent particles are present in simple cubic unit cell?
A metal crystallises in bcc unit cell with edge length 'a'. What will be the volume of one atom?
If the edge of a body-centred unit cell is 360 pm, what will be the approximate radius of the atom present in it? (in pm)
Sodium crystallizes in bcc structure with radius 1.86 × 10−8 cm. What is the length of unit cell of sodium?
Consider the following unit cell.
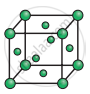
The number of particles (spheres) per unit cell is:
A metallic element has a cubic lattice with edge length of unit cell 2 Å. Calculate the number of unit cells in 200 g of the metal, if density of metal is 2.5 g cm-3?
The coordination number of atoms in body-centred cubic structure (bcc) is ______.
An element has a bee structure with unit cell edge length of 288 pm. How many unit cells and number of atoms are present in 200 g of the element?
A metal has an fcc lattice. The edge length of the unit cell is 404 pm. The density of the metal is 2.72 g cm−3. The molar mass of the metal is ______.
(NA Avogadro's constant = 6.02 × 1023 mol−1)
Identify unit cell from following having four particles in it
An element with molar mass 2.7 × 10-2 kg/mol. Forms a cubic units cell with edge length of 405 pm. If the density is 2.7 × 103 kg/m3. Find the nature of a cubic unit cell.
At room temperature, polonium Crystallises in a primitive cubic unit cell. If a = 3.36 Å. Calculate the theoretical density of polonium. [It's atomic weight is 209 g/mol.]
Silver crystallizes in the fcc structure. If the edge length of the unit cell is 400 pm, calculate the density of silver (Atomic mass of Ag = 108).
What is base centred (or end-centred) unit cell?
What would be the empirical formula of a compound having a unit cell containing A ion shared equally at the corner of the cube and B ion on the centre of faces of the cube?
