Advertisements
Advertisements
प्रश्न
Find the value of k for which the quadratic equation `9x^2-3kx+k=0` has equal roots.
उत्तर
It is given that the quadratic equation `9x^2-3kx+k=0` has equal roots.
∴ `D=0`
⇒`(-3k)^2-4xx9xxk=0`
⇒`9k^2-36k=0`
⇒`9k(k-4)=0`
⇒`k=0 or k-4=0`
⇒`k=0 or k=4`
Hence, 0 and 4 are the required values of k.
APPEARS IN
संबंधित प्रश्न
Solve` 2x^2+ax-a^2=0`
Write the following equation in the form ax2 + bx + c= 0, then write the values of a, b, c for the equation.
3m2 = 2m2 – 9
Pratik takes 8 hours to travel 36 km downstream and return to the same spot. The speed of boat in still water is 12 km. per hour. Find the speed of water current.
Choose the correct answer for the following question.
For \[\sqrt{2} x^2 - 5x + \sqrt{2} = 0\] find the value of the discriminant.
Mr. Dinesh owns an agricultural farm at village Talvel. The length of the farm is 10 meter more than twice the breadth. In order to harvest rain water, he dug a square shaped pond inside the farm. The side of pond is `1/3` of the breadth of the farm. The area of the farm is 20 times the area of the pond. Find the length and breadth of the farm and of the pond.
Solve the following quadratic equation.
`1/(x + 5) = 1/x^2`
Write the degree of Polynomial 5x2 + 2x + 3x4 + 4.
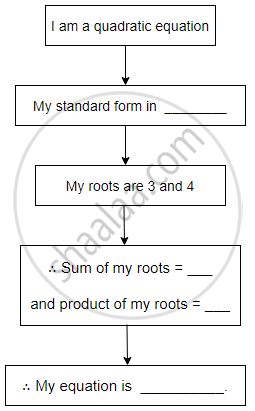
Complete the following activity to form a quadratic equation.
Activity:
In a right-angled triangle, altitude is 2 cm longer than its base. Find the dimensions of the right-angled triangle given that the length of its hypotenuse is 10 cm.

In the adjoining fig. `square` ABCD is a trapezium AB || CD and its area is 33 cm2. From the information given in the figure find the lengths of all sides of the `square` ABCD. Fill in the empty boxes to get the solution.
Solution: `square` ABCD is a trapezium.
AB || CD
`"A"(square "ABCD") = 1/2 ("AB" + "CD") xx`______
33 = `1/2 ("x" + 2"x" + 1) xx `______
∴ ______ = (3x + 1) × ______
∴ 3x2 +______ − ______ = 0
∴ 3x(______) + 10(______) = 0
∴ (3x + 10) (______) = 0
∴ (3x + 10) = 0 or ______ = 0
∴ x = `-10/3` or x = ______
But length is never negative.
∴ `"x" ≠ -10/3`
∴ x = ______
AB = ______, CD = ______, AD = BC = ______
