Advertisements
Advertisements
प्रश्न
Find a vector of magnitude of 5 units parallel to the resultant of the vectors \[\vec{a} = 2 \hat{i} + 3 \hat{j} - \hat{k} \text{ and } \vec{b} = \hat{i} - 2 \hat{j} +\widehat{k} .\]
उत्तर
Given the position vectors \[\vec{a} = 2 \hat{i} + 3 \hat{j} - \hat{k}\] and \[\vec{b} = \hat{i} - 2 \hat{j} + \hat{k}\]
∴ Resultant Vector = \[\vec{a} + \vec{b} = 2 \hat{i} + 3 \hat{j} - \hat{k} + \hat{i} - 2 \hat{j} + \hat{k} = 3 \hat{i} + \hat{j}\]
So, a unit vector parallel to the resultant vector is \[\frac{3 \hat{i} + \hat{j}}{\left| 3 \hat{i} + \hat{j} \right|} = \frac{3 \hat{i} + \hat{j}}{\sqrt{3^2 + 1^2}} = \frac{3 \hat{i} + \hat{j}}{\sqrt{10}}\]
Hence, required vector = \[5 \times \frac{\left( 3 \hat{i} + \hat{j} \right)}{\sqrt{10}} = \sqrt{\frac{5}{2}}\left( 3 \hat{i} + \hat{j} \right)\]
APPEARS IN
संबंधित प्रश्न
Find `|veca| and |vecb|`, if `(veca + vecb).(veca -vecb) = 8 and |veca| = 8|vecb|.`
Find a vector of magnitude 5 units, and parallel to the resultant of the vectors `veca = 2i + 3hatj - hatk` and `vecb = hati - 2hatj + hatk`.
Represent the following graphically:
(i) a displacement of 40 km, 30° east of north
(ii) a displacement of 50 km south-east
(iii) a displacement of 70 km, 40° north of west.
Find the magnitude of the vector \[\vec{a} = 2 \hat{i} + 3 \hat{j} - 6 \hat{k} .\]
Find the unit vector in the direction of \[3 \hat{i} + 4 \hat{j} - 12 \hat{k} .\]
If the sum of two unit vectors is a unit vector prove that the magnitude of their difference is `sqrt(3)`.
If \[\vec{a} = \hat{i} + \hat{j} + \hat{k} , \vec{b} = 4 \hat{i} - 2 \hat{j} + 3 \hat{k} \text { and } \vec{c} = \hat{i} - 2 \hat{j} + \hat{k} ,\] find a vector of magnitude 6 units which is parallel to the vector \[2 \vec{a} - \vec{b} + 3 \vec{c .}\]
Define "zero vector".
Write a vector of magnitude 12 units which makes 45° angle with X-axis, 60° angle with Y-axis and an obtuse angle with Z-axis.
Write the length (magnitude) of a vector whose projections on the coordinate axes are 12, 3 and 4 units.
Find a vector in the direction of \[\overrightarrow{a} = 2 \hat{i} - \hat{j} + 2 \hat{k} ,\] which has magnitude of 6 units.
Write two different vectors having same magnitude.
Write a vector in the direction of vector \[5 \hat{i} - \hat{j} + 2 \hat{k}\] which has magnitude of 8 unit.
Find a vector in the direction of vector \[2 \hat{i} - 3 \hat{j} + 6 \hat{k}\] which has magnitude 21 units.
If in a ∆ABC, A = (0, 0), B = (3, 3 \[\sqrt{3}\]), C = (−3\[\sqrt{3}\], 3), then the vector of magnitude 2 \[\sqrt{2}\] units directed along AO, where O is the circumcentre of ∆ABC is
Find all vectors of magnitude `10sqrt(3)` that are perpendicular to the plane of `hat"i" + 2hat"j" + hat"k"` and `-hat"i" + 3hat"j" + 4hat"k"`
Prove that in a ∆ABC, `sin"A"/"a" = sin"B"/"b" = sin"C"/"c"`, where a, b, c represent the magnitudes of the sides opposite to vertices A, B, C, respectively.
Find a vector of magnitude 6, which is perpendicular to both the vectors `2hat"i" - hat"j" + 2hat"k"` and `4hat"i" - hat"j" + 3hat"k"`.
The vector in the direction of the vector `hat"i" - 2hat"j" + 2hat"k"` that has magnitude 9 is ______.
Let `vecalpha = hati + 2hatj - hatk, vecbeta = 2hati - hatj + 3hatk, vecγ = 2hati + hatj + 6hatk`. If `vecalpha` and `vecbeta` are both perpendicular to a vector `vecδ` and `vecδ. vecγ` = 10, then the magnitude of `vecδ` is
If the sum of two-unit vectors is a unit vector, then the magnitude of their difference is
The area under a velocity-time curve represents the change in ______?
In a triangle ABC three forces of magnitudes `3vec(AB), 2vec(AC)` and `6vec(CB)` are acting along the sides AB, AC and CB respectively. If the resultant meets AC at D, then the ratio DC : AD will be equal to :
The magnitude of the vector `6hati - 2hatj + 3hatk` is ______.
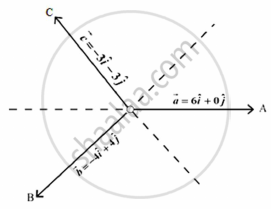
Read the following passage and answer the questions given below:
|
Teams A, B, C went for playing a tug of war game. Teams A, B, C have attached a rope to a metal ring and is trying to pull the ring into their own area. Team A pulls with force F1 = `6hati + 0hatj kN`, Team B pulls with force F2 = `-4hati + 4hatj kN`, Team C pulls with force F3 = `-3hati - 3hatj kN`,
|
- What is the magnitude of the force of Team A ?
- Which team will win the game?
- Find the magnitude of the resultant force exerted by the teams.
OR
In what direction is the ring getting pulled?
Find a vector of magnitude 20 units parallel to the vector `2hati + 5hatj + 4hatk`.
Find a vector of magnitude 9 units and perpendicular to the vectors.
`veca = 4hati - hatj + hatk` and `vecb = -2hati + hatj - 2hatk`