Advertisements
Advertisements
प्रश्न
Read the following passage and answer the questions given below:
|
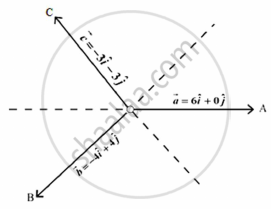
Teams A, B, C went for playing a tug of war game. Teams A, B, C have attached a rope to a metal ring and is trying to pull the ring into their own area. Team A pulls with force F1 = `6hati + 0hatj kN`, Team B pulls with force F2 = `-4hati + 4hatj kN`, Team C pulls with force F3 = `-3hati - 3hatj kN`,
|
- What is the magnitude of the force of Team A ?
- Which team will win the game?
- Find the magnitude of the resultant force exerted by the teams.
OR
In what direction is the ring getting pulled?
उत्तर
We have,
`|vecF_1| = sqrt(6^2 + 0^2)` = 6 kN,
`|vecF_2| = sqrt((-4)^2 + 4^2) = sqrt(32) = 4sqrt(2) kN`,
`|vecF_3| = sqrt((-3)^2 + (-3)^2) = sqrt(18) = 3sqrt(2) kN`.
i. Magnitude of force of Team A = 6 kN.
ii. Since `veca + vecc = 3(hati - hatj)` and `vecb = -4(hati - hatj)`
So, `vecb` and `veca + vecc` are unlike vectors having same intial point
and `|vecb| = 4sqrt(2)` and `|veca + vecc| = 3sqrt(2)`
Thus `|vecF_2| > |vecF_1 + vecF_3|` also `vecF_2` and `vecF_1 + vecF_3` are unlike
Hence B will win the game
iii. `vecF = vecF_1 + vecF_2 + vecF_3`
= `6hati + 0hatj - 4hati + 4hatj - 3hati - 3hatj`
= `-hati + hatj`
∴ `|vecF| = sqrt((-1)^2 + (1)^2) = sqrt(2) kN`.
OR
`vecF = -hati + hatj`
∴ θ = `π - tan^-1 (1/1)`
= `π - π/4`
= `(3π)/4`; where 'θ' is the angle made by the resultant force with the +ve direction of the x-axis.
APPEARS IN
संबंधित प्रश्न
If `veca` is a nonzero vector of magnitude 'a' and λ a nonzero scalar, then λ`veca` is unit vector if ______.
Find a vector of magnitude 5 units, and parallel to the resultant of the vectors `veca = 2i + 3hatj - hatk` and `vecb = hati - 2hatj + hatk`.
If `veca, vecb, vecc` are mutually perpendicular vectors of equal magnitudes, show that the vector `veca + vecb+ vecc` is equally inclined to `veca, vecb` and `vecc`.
If `veca, vecb, vecc` are mutually perpendicular vectors of equal magnitudes, find the angle which `veca + vecb + vecc`make with `veca or vecb or vecc`
Represent the following graphically:
(i) a displacement of 40 km, 30° east of north
(ii) a displacement of 50 km south-east
(iii) a displacement of 70 km, 40° north of west.
Find the magnitude of the vector \[\vec{a} = 2 \hat{i} + 3 \hat{j} - 6 \hat{k} .\]
Find the unit vector in the direction of \[3 \hat{i} + 4 \hat{j} - 12 \hat{k} .\]
If \[\vec{a} = \hat{i} + \hat{j} + \hat{k} , \vec{b} = 4 \hat{i} - 2 \hat{j} + 3 \hat{k} \text { and } \vec{c} = \hat{i} - 2 \hat{j} + \hat{k} ,\] find a vector of magnitude 6 units which is parallel to the vector \[2 \vec{a} - \vec{b} + 3 \vec{c .}\]
Find a vector of magnitude of 5 units parallel to the resultant of the vectors \[\vec{a} = 2 \hat{i} + 3 \hat{j} - \hat{k} \text{ and } \vec{b} = \hat{i} - 2 \hat{j} +\widehat{k} .\]
Find a vector \[\vec{r}\] of magnitude \[3\sqrt{2}\] units which makes an angle of \[\frac{\pi}{4}\] and \[\frac{\pi}{4}\] with y and z-axes respectively.
Define "zero vector".
Find a vector in the direction of \[\overrightarrow{a} = 2 \hat{i} - \hat{j} + 2 \hat{k} ,\] which has magnitude of 6 units.
Find a vector \[\overrightarrow{a}\] of magnitude \[5\sqrt{2}\], making an angle of \[\frac{\pi}{4}\] with x-axis, \[\frac{\pi}{2}\] with y-axis and an acute angle θ with z-axis.
Find a vector in the direction of vector \[2 \hat{i} - 3 \hat{j} + 6 \hat{k}\] which has magnitude 21 units.
If in a ∆ABC, A = (0, 0), B = (3, 3 \[\sqrt{3}\]), C = (−3\[\sqrt{3}\], 3), then the vector of magnitude 2 \[\sqrt{2}\] units directed along AO, where O is the circumcentre of ∆ABC is
Prove that in a ∆ABC, `sin"A"/"a" = sin"B"/"b" = sin"C"/"c"`, where a, b, c represent the magnitudes of the sides opposite to vertices A, B, C, respectively.
The vector in the direction of the vector `hat"i" - 2hat"j" + 2hat"k"` that has magnitude 9 is ______.
Let `vecalpha = hati + 2hatj - hatk, vecbeta = 2hati - hatj + 3hatk, vecγ = 2hati + hatj + 6hatk`. If `vecalpha` and `vecbeta` are both perpendicular to a vector `vecδ` and `vecδ. vecγ` = 10, then the magnitude of `vecδ` is
Which of the following statements is false about forces/ couple?
In a triangle ABC three forces of magnitudes `3vec(AB), 2vec(AC)` and `6vec(CB)` are acting along the sides AB, AC and CB respectively. If the resultant meets AC at D, then the ratio DC : AD will be equal to :
The magnitude of the vector `6hati - 2hatj + 3hatk` is ______.
Find a vector of magnitude 20 units parallel to the vector `2hati + 5hatj + 4hatk`.
Find a vector of magnitude 9 units and perpendicular to the vectors.
`veca = 4hati - hatj + hatk` and `vecb = -2hati + hatj - 2hatk`