Advertisements
Advertisements
प्रश्न
For the pair of linear equations given below, draw graphs and then state, whether the lines drawn are parallel or perpendicular to each other.
2x - 3y = 6
`x/(2) + y/(3) = 1`
उत्तर
To draw the graph of 2x - 3y = 6 and `x/(2) + y/(3) = 1` follows the steps:
First prepare a table as below:
| X | -1 | 0 | 1 |
| Y = `(2)/(3) xx 2` | `-(8)/(3)` | -2 | `-(4)/(3)` |
| Y = `-(3)/(2) xx + 3` | `(9)/(2)` | 3 | `(3)/(2)` |
Now sketch the graph as shown:
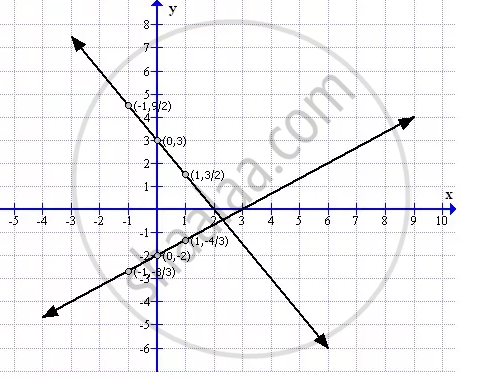
From the graph it can verify that the lines are perpendicular.
APPEARS IN
संबंधित प्रश्न
Draw the graph of the equation given below.
2x + y = 1
The following distribution gives the daily income of 50 workers of a factory.
| Daily income (in ₹) | 200-220 | 220-240 | 240-260 | 260-280 | 280-300 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Convert the distribution above to a 'less than type' cumulative frequency distribution and draw its ogive.
Draw the graph for the linear equation given below:
x + 3 = 0
Draw the graph for the linear equation given below:
y + 6 = 0
Draw the graph for the linear equation given below:
4x - y = 0
Draw the graph for the equation given below:
3x + 2y = 6
On the same graph paper, plot the graph of y = x - 2, y = 2x + 1 and y = 4 from x= - 4 to 3.
Draw a graph of each of the following equations: x = -3y
Draw a graph of the equation 2x - 3y = 15. From the graph find the value of:
(i) x, when y = 3
(ii) y, when x = 0
Draw a graph of the equation 5x - 3y = 1. From the graph find the value of:
(i) x, when y = 8
(ii) y, when x = 2
