Advertisements
Advertisements
प्रश्न
Four resistances of 2.0Ω each are joined end to end, to form a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent comers.
उत्तर
The diagram indicates a square ABCD formed by joining four resistances of 2Ω each, end to end.
Let us calculate the equivalent resistance of the combination B between the two adjacent comets C and D.
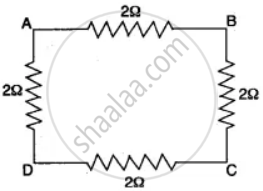
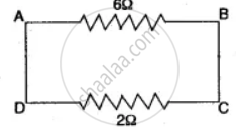
From given figure, arms DA, AB and BC are joined in series.
So, their equivalent of 6Ω and 2Ω are in parallel.
∴ The equivalent resistance of the combination is R.
Then, `1/"R" = 1/6 + 1/2 = 4/6 = 2/3`
∴ R = `3/2` Ω
= 1.5 Ω
APPEARS IN
संबंधित प्रश्न
In series combination which remains constant?
(a) Voltage
(b) Current
(c) Both current and voltage
(d) Both are variables
A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R’, then the ratio `"R"/"R'"` is ______.
How does the resistance of a pure metal change if its temperature decreases?
What possible values of resultant resistance one can get by combining two resistances, one of value 2 ohm and the other 6 ohm?
Calculate the combined resistance in each case:
A p.d. of 4 V is applied to two resistors of 6 Ω and 2 Ω connected in series. Calculate:
(a) the combined resistance
(b) the current flowing
(c) the p.d. across the 6 Ω resistor
You are supplied with a number of 100 Ω resistors. How could you combine some of these resistors to make a 250 Ω resistor?
Choose the correct alternative and rewrite the following:
You are given three equal resistances. In how many combinations can they are arranged?
Three resistors of 6Ω, 3Ω and 2Ω are connected together so that their total resistance is greater than 6Ω but less than 8Ω Draw a diagram to show this arrangement and calculate its total resistance.
If the current I through a resistor is increased by 100% (assume that temperature remains unchanged), the increase in power dissipated will be:
