Advertisements
Advertisements
Question
Four resistances of 2.0Ω each are joined end to end, to form a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent comers.
Solution
The diagram indicates a square ABCD formed by joining four resistances of 2Ω each, end to end.
Let us calculate the equivalent resistance of the combination B between the two adjacent comets C and D.
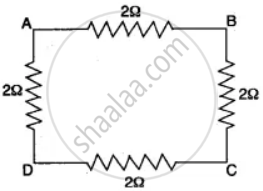
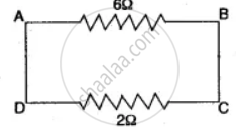
From given figure, arms DA, AB and BC are joined in series.
So, their equivalent of 6Ω and 2Ω are in parallel.
∴ The equivalent resistance of the combination is R.
Then, `1/"R" = 1/6 + 1/2 = 4/6 = 2/3`
∴ R = `3/2` Ω
= 1.5 Ω
APPEARS IN
RELATED QUESTIONS
In series combination which remains constant?
(a) Voltage
(b) Current
(c) Both current and voltage
(d) Both are variables
A p.d. of 4 V is applied to two resistors of 6 Ω and 2 Ω connected in series. Calculate:
(a) the combined resistance
(b) the current flowing
(c) the p.d. across the 6 Ω resistor
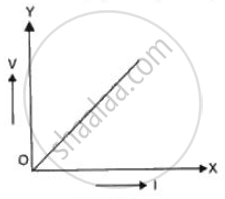
A graph is plotted taking p.d. along y-axis and electric current along x-axis. Name the physical quantity that represents the slope of this graph (Fig.).
You have three resistors of values 2 `Omega`, 3 `Omega`, and 5 `Omega`. How will you join them so that the total resistance is less than 2 `Omega`?
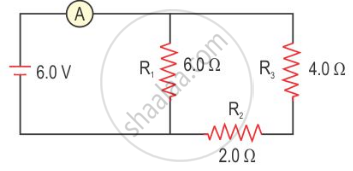
Three resistors of 6.0 Ω, 2.0 Ω and 4.0 Ω are joined to an ammeter A and a cell of emf 6.0 V as shown in the following figure. Calculate :
- the effective resistance of the circuit.
- the reading of ammeter.
What do you mean by power rating of an electrical appliance? How do you use it to calculate
(a) the resistance of the appliance and
(b) the safe limit of the current in it, while in use?
State a relation between electrical power, resistance and potential difference in an electrical circuit.
What should be the length of a nickel wire of area of cross-section 3 mm2 used for making a rheostat of 750 ohm? (ρ of nickle = 0.069 Ohm mm2/m)
Two wires of the same length and area made of two materials of resistivity ρ1 and ρ2 are connected in series to a source of potential V. The equivalent resistivity for the same area is:
