Advertisements
Advertisements
प्रश्न
(i) Find the reflection of the point (3, 5) on X-axis.
(ii) Find the reflection of the point (- 3, 5) on X-axis.
(iii) Find the reflection of the point (- 3, – 5) on X-axis.
(iv) Find the reflection of the point (3, – 5) on X-axis.
उत्तर
(i) \[\ce{A(3, 5)->[Mx][]D(3, -5)}\]
(ii) \[\ce{B(-3, 5)->[Mx][]C(-3, -5)}\]
(iii) \[\ce{C(-3, -5)->[Mx][]B(-3, 5)}\]
(iv) \[\ce{D(3, 5)->[Mx][]A(3, -5)}\]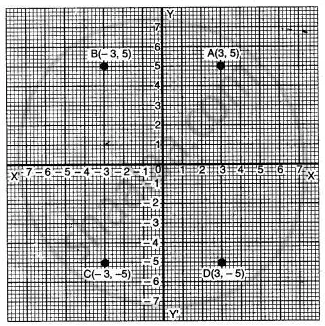
APPEARS IN
संबंधित प्रश्न
State the co-ordinates of the following point under reflection in the line x = 0:
(–6, 4)
The point A(–3, 2) is reflected in the x-axis to the point A’. Point A’ is then reflected in the origin to point A”.
- Write down the co-ordinates of A”.
- Write down a single transformation that maps A onto A”.
P' is the image of P under reflection in the x-axis. If the co-ordinates of P' are (2, 10), write the co-ordinates of P.
Find the co-ordinates of the image of A (-5, 4) after reflection in the line
y = 0
Find the co-ordinates of the image of A (-5, 4) after reflection in the line
y = 4
Find the co-ordinates of the image of S(4,-1) after reflection in the line
x = 0
Find the co-ordinates of the image of S(4,-1) after reflection in the line
y = 5
Point A (1,-5) is mapped as A' on reflection in the line y= l . The point B (-5, 1) is mapped as B' on reflection in the line y=4. Write the co-ordinates of A' and B'. Calculate AB'.
Using a graph paper, plot the points A (6,4) and B (0,4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for. the figure ABA’B’.
(iv) Find its perimeter.
(i) Point P(a, b) reflected on the X-axis to P'(5, 2). Write down the value of a and b.
(ii) P” is the image of P when reflected on the Y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”.
