Question

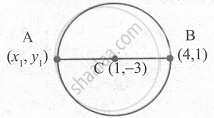
If (4, 1) is one extremity of a diameter of the circle x² + y² - 2x + 6y - 15 = 0 find the other extremity.

Answer 1

Given equation of the circle is x² + y² - 2x + 6y - 15 = 0

∴ 2g = - 2

⇒ g = - 1

∴ 2f = 6

⇒ f = 3 

⇒ c = - 5

Centre of the circle is (-g , -f) centre is c(1, -3)

Let A (x₁, y₁) be the other extremity of the diameter and B(4, 1) is one extremity.

Now, c is the mid-point of AB.

Mid point between the two points `((x_1 + x_2)/2, (y_1 + y_2)/2)`

∴ (1, -3) = `((x_1 + 4)/2, (y_1 + 1)/2)`   ...[Using mid-point formula]

Equating the x and y co-ordinates on both sides we get,

`1 = (x_1 + 4)/2`

⇒ 2 = x₁ + 4

⇒ x₁ = - 2

`- 3 = (y_1 + 1)/2`

⇒ - 6 = y₁ + 1

⇒ y₁ = - 6 - 1 = - 7

∴ The other extremity of the diameter is (-2, -7)