Advertisements
Advertisements
Question
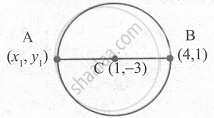
If (4, 1) is one extremity of a diameter of the circle x2 + y2 - 2x + 6y - 15 = 0 find the other extremity.
Solution
Given equation of the circle is x2 + y2 - 2x + 6y - 15 = 0
∴ 2g = - 2
⇒ g = - 1
∴ 2f = 6
⇒ f = 3
⇒ c = - 5
Centre of the circle is (-g , -f) centre is c(1, -3)
Let A (x1, y1) be the other extremity of the diameter and B(4, 1) is one extremity.
Now, c is the mid-point of AB.
Mid point between the two points `((x_1 + x_2)/2, (y_1 + y_2)/2)`
∴ (1, -3) = `((x_1 + 4)/2, (y_1 + 1)/2)` ...[Using mid-point formula]
Equating the x and y co-ordinates on both sides we get,
`1 = (x_1 + 4)/2`
⇒ 2 = x1 + 4
⇒ x1 = - 2
`- 3 = (y_1 + 1)/2`
⇒ - 6 = y1 + 1
⇒ y1 = - 6 - 1 = - 7
∴ The other extremity of the diameter is (-2, -7)
APPEARS IN
RELATED QUESTIONS
Find the centre and radius of the circle
x2 + y2 – 22x – 4y + 25 = 0
Find the equation of the circle passing through the points (0, 1), (4, 3) and (1, -1).
Find the value of P if the line 3x + 4y – P = 0 is a tangent to the circle x2 + y2 = 16.
(1, -2) is the centre of the circle x2 + y2 + ax + by – 4 = 0, then its radius:
If the centre of the circle is (-a, -b) and radius is `sqrt("a"^2 - "b"^2)` then the equation of circle is:
Find the equation of the circles with centre (2, 3) and passing through the intersection of the lines 3x – 2y – 1 = 0 and 4x + y – 27 = 0
Determine whether the points (– 2, 1), (0, 0) and (– 4, – 3) lie outside, on or inside the circle x2 + y2 – 5x + 2y – 5 = 0
Choose the correct alternative:
The equation of the circle passing through (1, 5) and (4, 1) and touching y-axis `x^2 + y^2 - 5x - 6y + 9 + lambda(4x + 3y - 19)` = where `lambda` is equal to
Choose the correct alternative:
The circle x2 + y2 = 4x + 8y + 5 intersects the line 3x – 4y = m at two distinct points if
Choose the correct alternative:
If the normals of the parabola y2 = 4x drawn at the end points of its latus rectum are tangents to the circle (x – 3)2 + (y + 2)2 = r2, then the value of r2 is
