Advertisements
Advertisements
प्रश्न
If f(x) = |x + 100| + x2, test whether f’(–100) exists.
उत्तर
f(x) = |x + 100| + x2
First let us find the left limit of f(x) at x = – 100
When x < – 100 ,
f(x) = – (x + 100) + x2
f(– 100) = – (– 100 + 100) + (– 100)2
f(– 100) = 1002
`f"'"(- 100^-) = lim_(x -> - 100^-) (f(x) - f(- 100))/(x - (- 100)`
= `lim_(x -> -10^-) (-(x + 100) + x^2 - 100^2)/(x + 100)`
= `lim_(x -> -100^-) [(-(x + 100))/(x + 100) + (x^2 - 100^2)/(x + 100)]`
= `lim_(x -> -100^-) [- 1 + ((x + 100)(x - 100))/(x + 100)]`
= `lim_(x -> -100^-) [- 1 + x - 100]`
= – 1 – 100 – 100
f'(– 100) = – 201 ........(1)
Next let us find the right limit of f(x) at x = – 100
when x > – 100
f(x) = x + 100 + x2
f(– 100) = – 100 + 100 + (– 100)2
f(– 100) = 1002
`f"'"(- 100^+) = lim_(x -> - 100^+) (f(x) - f(- 100))/(x - (- 100))`
= `lim_(x -> - 100^+) (x + 100 + x^2 - 100^2)/(x + 100)`
f'(– 100+) = – 199 ........(2)
From equation (1) and (2), we get
f’(– 100–) ≠ f'(– 100+)
∴ f’(x) does not exist at x = – 100
Hence, f'(– 100) does not exist
APPEARS IN
संबंधित प्रश्न
Find the derivatives of the following functions using first principle.
f(x) = 6
Determine whether the following function is differentiable at the indicated values.
f(x) = x |x| at x = 0
Determine whether the following function is differentiable at the indicated values.
f(x) = |x| + |x – 1| at x = 0, 1
Determine whether the following function is differentiable at the indicated values.
f(x) = sin |x| at x = 0
Show that the following functions are not differentiable at the indicated value of x.
`f(x) = {{:(-x + 2, x ≤ 2),(2x - 4, x > 2):}` , x = 2
Show that the following functions are not differentiable at the indicated value of x.
`f(x) = {{:(3x",", x < 0),(-4x",", x ≥ 0):}` , x = 0
The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.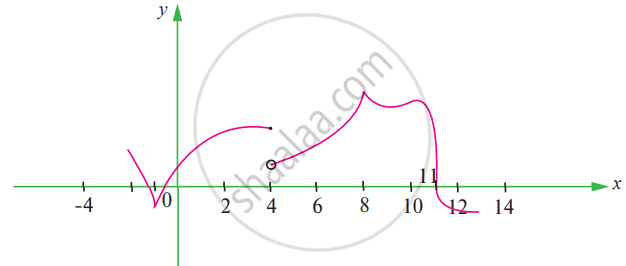
Choose the correct alternative:
f y = f(x2 + 2) and f'(3) = 5 , then `("d"y)/("d"x)` at x = 1 is
Choose the correct alternative:
If f(x) = x2 – 3x, then the points at which f(x) = f’(x) are
Choose the correct alternative:
If y = mx + c and f(0) = f’(0) = 1, then f(2) is
Choose the correct alternative:
If pv = 81, then `"dp"/"dv"` at v = 9 is
Choose the correct alternative:
It is given that f'(a) exists, then `lim_(x -> "a") (xf("a") - "a"f(x))/(x - "a")` is
Choose the correct alternative:
If f(x) = `{{:(x + 1, "when" x < 2),(2x - 1, "when" x ≥ 2):}` , then f'(2) is
Choose the correct alternative:
If g(x) = (x2 + 2x + 1) f(x) and f(0) = 5 and `lim_(x -> 0) (f(x) - 5)/x` = 4, then g'(0) is
Choose the correct alternative:
If f(x) = `{{:(x + 2, - 1 < x < 3),(5, x = 3),(8 - x, x > 3):}` , then at x = 3, f'(x) is
