Advertisements
Advertisements
प्रश्न
If the letters of the word ASSASSINATION are arranged at random. Find the probability that two I’s and two N’s come together
उत्तर
Total number of word is ASSASSINATION are 13.
Where, we have 3A’s, 4S’, 2I’s, 2N’s, 1T’s and 1O’s.
If 2I’s and 2N’s come together then there are 10 alphabets
Number of words when 2I’s and 2N’s are come together
= `(10!)/(3!4!) xx (4!)/(2!2!)`
∴ Required probability = `((10!)/(3!4!) xx (4!)/(2!2!))/((13!)/(3!4!2!2!))`
= `(4!10!)/(2!2!3!4!) xx (3!4!2!2!)/(13!)`
= `(4!10!)/(13!)`
= `(4 xx 3 xx 2 xx 10!)/(13 xx 12 xx 11 xx 10!)`
= `(4 xx 3 xx 2)/(13 xx 12 xx 11)`
= `2/143`
APPEARS IN
संबंधित प्रश्न
A coin is tossed twice, what is the probability that at least one tail occurs?
Three coins are tossed once. Find the probability of getting
- 3 heads
- 2 heads
- at least 2 heads
- at most 2 heads
- no head
- 3 tails
- exactly two tails
- no tail
- atmost two tails.
Check whether the following probabilities P(A) and P(B) are consistently defined
P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6
Check whether the following probabilities P(A) and P(B) are consistently defined
P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8
Fill in the blank in following table:
| P(A) | P(B) | P(A ∩ B) | P(A ∪ B) |
| `1/3` | `1/5` | `1/15` | .... |
4 cards are drawn from a well-shuffled deck of 52 cards. What is the probability of obtaining 3 diamonds and one spade?
From the employees of a company, 5 persons are selected to represent them in the managing committee of the company. Particulars of five persons are as follows:
| S. No. | Name | Sex | Age in years |
| 1. | Harish | M | 30 |
| 2. | Rohan | M | 33 |
| 3. | Sheetal | F | 46 |
| 4. | Alis | F | 28 |
| 5. | Salim | M | 41 |
A person is selected at random from this group to act as a spokesperson. What is the probability that the spokesperson will be either male or over 35 years?
If 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when, the digits are repeated?
Two unbiased dice are thrown. Find the probability that the total of the numbers on the dice is greater than 10.
Two unbiased dice are thrown. Find the probability that the sum of the numbers obtained on the two dice is neither a multiple of 2 nor a multiple of 3
If a letter is chosen at random from the English alphabet, find the probability that the letter is a vowel .
If a letter is chosen at random from the English alphabet, find the probability that the letter is a consonant .
In a lottery, a person chooses six different numbers at random from 1 to 20, and if these six numbers match with six number already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game?
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (i) | 0.1 | 0.01 | 0.05 | 0.03 | 0.01 | 0.2 | 0.6 |
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (iv) |
\[\frac{1}{14}\]
|
\[\frac{2}{14}\]
|
\[\frac{3}{14}\]
|
\[\frac{4}{14}\]
|
\[\frac{5}{14}\]
|
\[\frac{6}{14}\]
|
\[\frac{15}{14}\]
|
A box contains 100 bulbs, 20 of which are defective. 10 bulbs are selected for inspection. Find the probability that all 10 are good
Two dice are thrown together. The probability that neither they show equal digits nor the sum of their digits is 9 will be
An urn contains twenty white slips of paper numbered from 1 through 20, ten red slips of paper numbered from 1 through 10, forty yellow slips of paper numbered from 1 through 40, and ten blue slips of paper numbered from 1 through 10. If these 80 slips of paper are thoroughly shuffled so that each slip has the same probability of being drawn. Find the probabilities of drawing a slip of paper that is numbered 1, 2, 3, 4 or 5
An urn contains twenty white slips of paper numbered from 1 through 20, ten red slips of paper numbered from 1 through 10, forty yellow slips of paper numbered from 1 through 40, and ten blue slips of paper numbered from 1 through 10. If these 80 slips of paper are thoroughly shuffled so that each slip has the same probability of being drawn. Find the probabilities of drawing a slip of paper that is red or yellow and numbered 1, 2, 3 or 4
Six new employees, two of whom are married to each other, are to be assigned six desks that are lined up in a row. If the assignment of employees to desks is made randomly, what is the probability that the married couple will have nonadjacent desks?
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine P(A)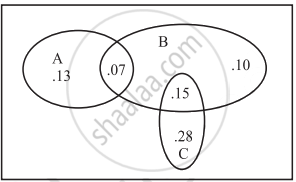
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine `P(A ∩ barB)`
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine Probability of exactly one of the three occurs
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that all the three balls are red
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that all one ball is red and two balls are white
6 boys and 6 girls sit in a row at random. The probability that all the girls sit together is ______.
The sum of probabilities of two students getting distinction in their final examinations is 1.2
A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?
