Advertisements
Advertisements
प्रश्न
If two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.
उत्तर
Let AB and AC be two chords and AOD be a diameter such that
∠ BAO = ∠ CAO
Draw OL ⊥ AB and OM ⊥ AC.
Now prove, Δ OLA = Δ OMA
Then OL = OM ⇒ AB = CD. .....(Chords which are equidistant from the centre are equal.)
Hence proved.
APPEARS IN
संबंधित प्रश्न
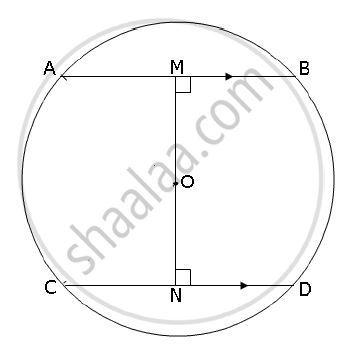
In the figure given below AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
In the following figure, O is the centre of the circle. Find the value of a, b, c and d.
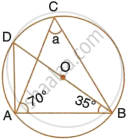
Calculate:
- ∠CDB,
- ∠ABC,
- ∠ACB.
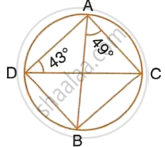
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.
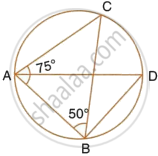
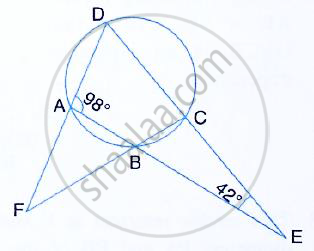
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; Calculate :
(i) ∠AFB (ii) ∠ADC
In following fig., chords PQ and RS of a circle intersect at T. If RS = 18cm, ST = 6cm and PT = 18cm, find the length of TQ.

In the figure, chords AE and BC intersect each other at point D. If AD = BD, show that AE = BC.
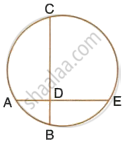
The line joining the midpoints of two chords of a circle passes through its center.
Prove that the chords are parallel.
The length of the common chord of two intersecting circles is 30 cm. If the diameters of these two circles are 50 cm and 34 cm, calculate the distance between their centers.
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
