Advertisements
Advertisements
प्रश्न
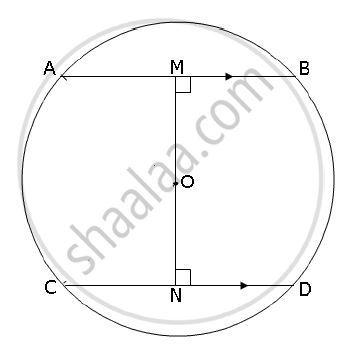
In the figure given below AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
उत्तर
Construction: Join OA and OB
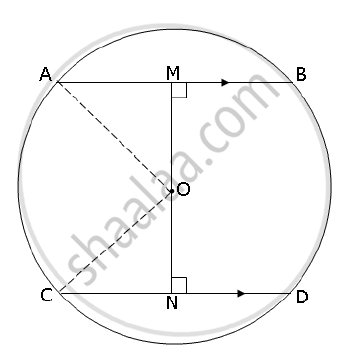
As OM ⊥ AB and ON ⊥ CD
∴ AM = MB = 24/2 cm = 12 cm
CN = ND = 18/2 cm = 9 cm
`:. OM = sqrt(OA^2 -AM^2) = sqrt(15^2 - 12^2) = 9 cm`
`ON = sqrt(OC^2 - CN^2) = sqrt(15^2 - 9^2 ) = 12 cm`
∴ MN = OM + ON = 9 + 12 = 21 cm
APPEARS IN
संबंधित प्रश्न
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
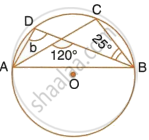
In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
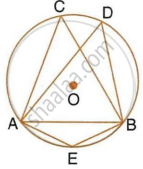
In the following figure, O is the centre of the circle. Find the values of a, b, c and d
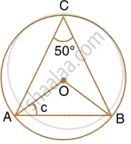
In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
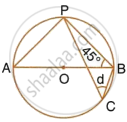
In the following figure, O is centre of the circle and ΔABC is equilateral.
Find:
- ∠ADB,
- ∠AEB.
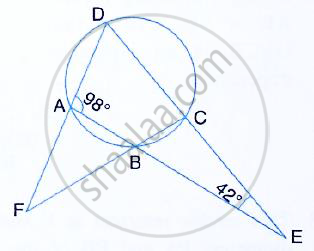
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; Calculate :
(i) ∠AFB (ii) ∠ADC
In following fig., chords PQ and RS of a circle intersect at T. If RS = 18cm, ST = 6cm and PT = 18cm, find the length of TQ.

In the figure, chords AE and BC intersect each other at point D. If AD = BD, show that AE = BC.
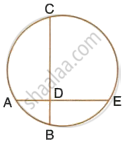
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
