Advertisements
Advertisements
प्रश्न
If U = {4, 7, 8, 10, 11, 12, 15, 16}, A = {7, 8, 11, 12} and B = {4, 8, 12, 15}, then verify De Morgan’s Laws for complementation
उत्तर
U = {4, 7, 8, 10, 11, 12, 15, 16}
A = {7, 8, 11, 12}
B = {4, 8, 12, 15}
De Morgan’s Laws for complementation.
(A ∪ B)’ = A’ ∩ B’
A ∪ B = {4, 7, 8, 11, 12, 15}
(A ∪ B)’ = {4, 7, 8, 10, 11, 12, 15, 16} – {4, 7, 8, 11, 12, 15}
= {10, 16} ...(1)
A’ = {4, 10, 15, 16}
B’ = {7, 10, 11, 16}
A’ ∩ B’ = {10, 16} ...(2)
From (1) and (2) it is verified that (A ∪ B)’ = A’ ∩ B’.
APPEARS IN
संबंधित प्रश्न
Using the adjacent Venn diagram, find the following set:
B – C
Using the adjacent Venn diagram, find the following set:
A’ ∪ B’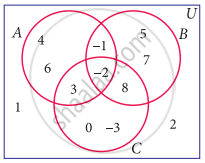
Using the adjacent Venn diagram, find the following set:
A’ ∩ B’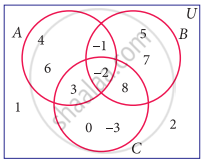
Using the adjacent Venn diagram, find the following set:
A – (B ∪ C)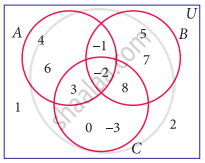
If K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h} then find the following:
(K ∪ L) ∩ (K ∪ M)
If A = {x : x ∈ Z, −2 < x ≤ 4}, B = {x : x ∈ W, x ≤ 5}, C = {− 4, −1, 0, 2, 3, 4} verify A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Verify A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) using Venn diagrams
If A = {b, c, e, g, h}, B = {a, c, d, g, i}, and C = {a, d, e, g, h}, then show that A – (B ∩ C) = (A – B) ∪ (A – C)
If A = {– 2, 0, 1, 3, 5}, B = {–1, 0, 2, 5, 6} and C = {–1, 2, 5, 6, 7}, then show that A – (B ∪ C) = (A – B) ∩ (A – C)
If A = `{y : y = ("a"+1)/2, "a" ∈ "W" and "a" ≤ 5}`, B = `{y : y = (2"n" – 1)/2, "n" ∈ "W" and "n" < 5}` and C = `{-1, −1/2, 1, 3/2, 2}` then show that A – (B ∪ C) = (A – B) ∩ (A – C)
