Advertisements
Advertisements
प्रश्न
In a class of 200 students who appeared in certain examinations, 35 students failed in CET, 40 in NEET and 40 in JEE, 20 failed in CET and NEET, 17 in NEET and JEE, 15 in CET and JEE, and 5 failed in all three examinations. Find how many students, failed in NEET or JEE entrance
उत्तर
Let A = set of students who failed in CET
B = set of students who failed in NEET
C = set of students who failed in JEE
X = set of all students
∴ n(X) = 200, n(A) = 35, n(B) = 40, n(C) = 40, (A ∩ B) = 20, n(B ∩ C) = 17, n(A ∩ C) = 15, n(A ∩ B ∩ C) = 5
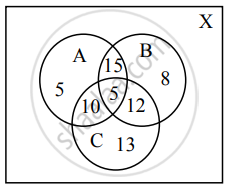
No. of students who failed in NEET or JEE entrance
= n(B ∪ C)
= n(B) + n(C) – n(B ∩ C)
= 40 + 40 – 17
= 63
APPEARS IN
संबंधित प्रश्न
Identify whether the following is set or not? Justify your answer.
The collection of all months of a year beginning with the letter J.
Identify whether the following is set or not? Justify your answer.
The collection of all boys in your class.
Identify whether the following is set or not? Justify your answer.
A collection of most dangerous animals of the world.
Write the following set in roster form:
D = {x : x is a prime number which is divisor of 60}
Write the following set in roster form:
E = The set of all letters in the word TRIGONOMETRY
Write the following set in the set-builder form:
{2, 4, 8, 16, 32}
Write the following set in the set-builder form:
{5, 25, 125, 625}
Which of the following collection are sets? Justify your answer:
The collection of difficult topics in mathematics.
Which of the following collection are sets? Justify your answer:
The collection of all question in this chapter.
Describe the following sets in Roster form:
{x : x is a letter before e in the English alphabet}
Describe the following sets in Roster form:
{x ∈ N : x = 2n, n ∈ N};
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a, b \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ c, d \right\} \subset A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[a \in A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\left\{ 6, 7, 8 \right\} \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[\left\{ 1 \right\} \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\]Which of the following are true? \[\left\{ 1 \right\} \in A\]
Write down all possible proper subsets each of the following set:
{1, 2, 3}
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
4 _____ A
Describe the following set in Roster form
A = {x/x is a letter of the word 'MOVEMENT'}
Describe the following set in Roster form
B = `{x//x "is an integer", -3/2 < x < 9/2}`
In a class of 200 students who appeared in certain examinations, 35 students failed in CET, 40 in NEET and 40 in JEE, 20 failed in CET and NEET, 17 in NEET and JEE, 15 in CET and JEE, and 5 failed in all three examinations. Find how many students, did not fail in any examination.
In a hostel, 25 students take tea, 20 students take coffee, 15 students take milk, 10 students take bot tea and coffee, 8 students take both milk and coffee. None of them take tea and milk both and everyone takes at least one beverage, find the total number of students in the hostel.
There are 260 persons with skin disorders. If 150 had been exposed to chemical A, 74 to chemical B, and 36 to both chemicals A and B, find the number of persons exposed to Chemical A but not Chemical B
Write the following interval in Set-Builder form
(2, 5]
A college awarded 38 medals in volleyball, 15 in football, and 20 in basketball. The medals awarded to a total of 58 players and only 3 players got medals in all three sports. How many received medals in exactly two of the three sports?
Select the correct answer from given alternative.
In a city 20% of the population travels by car, 50% travels by bus and 10% travels by both car and bus. Then, persons travelling by car or bus are
State which of the following statement are true and which are false. Justify your answer.
7,747 ∈ {t | t is a multiple of 37}
Write the following sets in the roaster from:
A = {x : x ∈ R, 2x + 11 = 15}
State which of the following statement is true and which is false. Justify your answer.
35 ∈ {x | x has exactly four positive factors}.
128 ∈ {y | the sum of all the positive factors of y is 2y}
Determine whether the following statement is true or false. Justify your answer.
For all sets A, B, and C, A – (B – C) = (A – B) – C
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in English and Mathematics but not in Science.
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study Sanskrit only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study at least one of the three languages
If sets A and B are defined as A = `{(x, y) | y = 1/x, 0 ≠ x ∈ "R"}` B = {(x, y) | y = – x, x ∈ R}, then ______.
State True or False for the following statement.
Let sets R and T be defined as
R = {x ∈ Z | x is divisible by 2}
T = {x ∈ Z | x is divisible by 6}. Then T ⊂ R
