Advertisements
Advertisements
प्रश्न
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in English and Mathematics but not in Science.
उत्तर
Let the number of students who passed in Mathematics M, E be in English and S be in Science.
Then n(U) = 100
n(M) = 12
n(E) = 15
n(S) = 8
n(E ∩ M) = 6
n(M ∩ S) = 7
n(E ∩ S) = 4
And n(E ∩ M ∩ S) = 4
Let us draw a Venn diagram.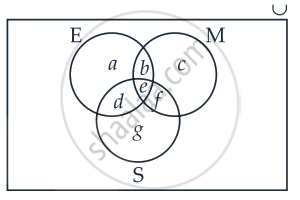
According to the Venn diagram, we get
a + b + d + e = 15 ......(i)
b + c + e + f = 12 ......(ii)
d + e + f + g = 8 .....(iii)
n(E ∩ M) = 6
∴ b + e = 6 ......(iv)
n(M ∩ S) = 7
∴ e + f = 7 ......(v)
n(E ∩ S) = 4
∴ d + e = 4 ......(vi)
And n(E ∩ M ∩ S) = 4
∴ e = 4 ......(vii)
From equations (iv) and (vii)
We get b + 4 = 6
∴ b = 2
From equations (v) and (vii)
We get 4 + f = 7
∴ f = 3
From equations (vi) and (vii)
We get d + 4 = 4
∴ d = 0
From equation (i) we get
a + b + d + e = 15
⇒ a + 2 + 0 + 4 = 15
⇒ a = 9
From equation (ii)
b + c + e + f = 12
⇒ 2 + c + 4 + 3 = 12
⇒ c = 3
From equation (iii)
d + e + f + g = 8
⇒ 0 + 4 + 3 + g = 8
⇒ g = 1
∴ The number of students who passed in English and Mathematics but not in Science, b = 2.
APPEARS IN
संबंधित प्रश्न
Write the following set in roster form:
A = {x : x is an integer and –3 ≤ x < 7}
Write the following set in the set-builder form:
{5, 25, 125, 625}
List all the elements of the following set:
A = {x : x is an odd natural number}
List all the elements of the following set:
E = {x : x is a month of a year not having 31 days}
List all the elements of the following set:
F = {x : x is a consonant in the English alphabet which precedes k}.
Which of the following collection are sets? Justify your answer:
The collection of all girls in your class.
Describe the following sets in set-builder form:
B={1,1/2 ,1/3, 1/4,1/5,...........};
Match each of the sets on the left in the roster form with the same set on the right described in the set-builder form:
| (i) | {A, P, L, E} | (i) | x : x + 5 = 5, x ∈ Z |
| (ii) | {5, −5} | (ii) | {x : x is a prime natural number and a divisor of 10} |
| (iii) | {0} | (iii) | {x : x is a letter of the word "RAJASTHAN"} |
| (iv) | {1, 2, 5, 10,} | (iv) | {x: x is a natural number and divisor of 10} |
| (v) | {A, H, J, R, S, T, N} | (v) | x : x2 − 25 = 0 |
| (vi) | {2, 5} | (vi) | {x : x is a letter of the word "APPLE"} |
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a \right\} \subset \left\{ \left\{ a \right\}, b \right\}\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[a \in A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ a, b, c \right\} \subset A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\left\{ \left\{ 4, 5 \right\} \right\} \subset A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\phi \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\]Which of the following are true? \[\left\{ \left\{ 2 \right\}, \left\{ 1 \right\} \right\} \not\subset A\]
Let \[\left\{ \left\{ 2 \right\}, \left\{ 1 \right\} \right\} \not\subset A\] Which of the following are true? \[\left\{ \left\{ 2 \right\}, \left\{ 1 \right\} \right\} \not\subset A\]
Write down all possible proper subsets each of the following set:
{1, 2, 3}
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
4 _____ A
Describe the following set in Roster form
B = `{x//x "is an integer", -3/2 < x < 9/2}`
Describe the following set in Set-Builder form
{0, ±1, ±2, ±3}
From amongst 2000 literate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read Only one of the newspapers
Write the following sets in the roaster from:
C = {x | x is a positive factor of a prime number p}
Write the following sets in the roaster form:
D = {t | t3 = t, t ∈ R}
If Y = {x | x is a positive factor of the number 2p – 1 (2p – 1), where 2p – 1 is a prime number}.Write Y in the roaster form.
State which of the following statements is true and which is false. Justify your answer.
496 ∉ {y | the sum of all the positive factors of y is 2y}.
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English and Sanskrit but not French
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French and Sanskrit but not English
Let S = {x | x is a positive multiple of 3 less than 100}
P = {x | x is a prime number less than 20}. Then n(S) + n(P) is ______.
The set {x ∈ R : 1 ≤ x < 2} can be written as ______.
