Advertisements
Advertisements
प्रश्न
In a solid if F = V = 5, then the number of edges in this shape is ______.
पर्याय
6
4
8
2
उत्तर
In a solid if F = V = 5, then the number of edges in this shape is 8.
Explanation:
Euler's formula for any polyhedron is F + V – R = 2
Given, F = V = 5
On putting the values of F and V in the Euler's formula, we get
5 + 5 – E = 2
⇒ 10 – E = 2
⇒ E = 8
Notes
F = Faces, V = Verticles and E = Edges
APPEARS IN
संबंधित प्रश्न
Verify Euler’s formula for the following three-dimensional figures:

Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
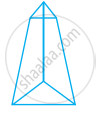
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
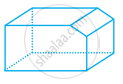
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
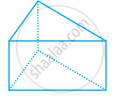
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
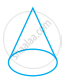
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
Using Euler’s formula, find the value of unknown x in the following table.
| Faces | 7 |
| Vertices | 10 |
| Edges | x |
Using Euler’s formula, find the value of unknown y in the following table.
| Faces | y |
| Vertices | 12 |
| Edges | 18 |
Check whether a polyhedron can have V = 12, E = 6 and F = 8.
A solid has forty faces and sixty edges. Find the number of vertices of the solid.
