Advertisements
Advertisements
प्रश्न
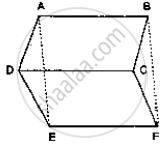
In the given below fig. ABCD, ABFE and CDEF are parallelograms. Prove that ar (ΔADE)
= ar (ΔBCF)
उत्तर
Given that,
ABCDis a parallelogram ⇒ AD = BC
CDEF is a parallelogram ⇒ DE = CF
ABFE is a parallelogram ⇒ AE = BF
Thus, in Δs ADE and BCF,we have
AD = BC,DE = CF and AE = BF
So, by SSS criterion of congruence, we have
ΔADE ≅ ΔABCF
∴ ar ( Δ ADE ) = ar ( BCF )
APPEARS IN
संबंधित प्रश्न
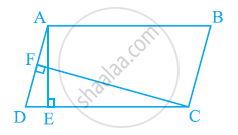
In the given figure, ABCD is parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
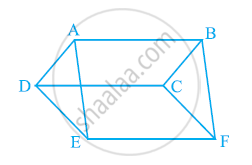
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
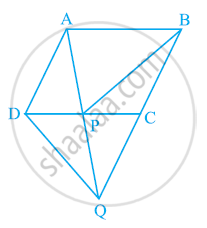
In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that
ar (BPC) = ar (DPQ).
[Hint: Join AC.]
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
In the following figure, PSDA is a parallelogram. Points Q and R are taken on PS such that PQ = QR = RS and PA || QB || RC. Prove that ar (PQE) = ar (CFD).

ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
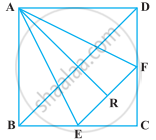
If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (Figure).
[Hint: Join BD and draw perpendicular from A on BD.]
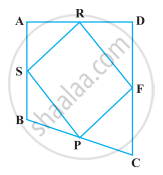
The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = `7/9` ar (XYBA)
