Advertisements
Advertisements
प्रश्न
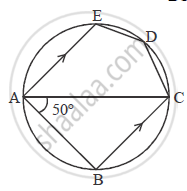
In the given figure, ABCDE is a pentagon inscribed in a circle such that AC is a diameter and side BC//AE.If
∠ BAC=50°, find giving reasons:
(i) ∠ACB
(ii) ∠EDC
(iii) ∠BEC
Hence prove that BE is also a diameter
उत्तर

Let ∠ACB be x, ∠EDC be y and ∠BEC as z.
Now, ∠ABC = 90° {Angle in a semi-circle}
(i) ∴ In ΔABC, ∠ABC + ∠BAC + ∠ACB = 180°
⇒ 90° + 50° + ∠ACB = 180°
∠ACB = 40° = x
(ii) Now, ∠EAC = ∠ACB {Alternate interior angles ∴ AC is transversal to the parallel lines AE & BC}
∴ ∠EAC = 40°
Also, ∠EAC + ∠EDC = 180°
∴ 40° + ∠EDC = 180°
⇒ ∠EDC = 140° = y
(iii) ∠EBC + ∠EDC = 180° {Angles in cyclic quadrilateral}
∠EBC + 140° = 180°
∠EBC = 40°
∴ In ΔEBC
∠BEC + ∠ECB + ∠EBC = 180°
∴ ∠BEC + 90° + 40° = 180°
∴ ∠BEC = 50°
Also in ΔEAB
∠EAB = ∠EAC + ∠BAC
= 40° + 50°
∠EAB = 90°
We know, if an angle of a triangle in a circle is 90o then, the hypotenuse must be the diameter of the circle. Hence, BE is the diameter of the circle.
APPEARS IN
संबंधित प्रश्न
Complete the following figure, about the given lines of symmetry which are shown by dotted lines and name the figure thus obtained:
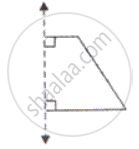
Complete the following figure, about the given lines of symmetry which are shown by dotted lines and name the figure thus obtained:
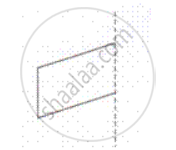
Draw the lines of symmetry of the following.
The number of lines of symmetry in a ruler is ______.
In figure, if B is the image of the point A with respect to the line l and P is any point lying on l, then the lengths of the line segments PA and PB are ______.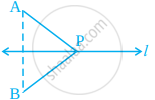
The number of lines of symmetry in a regular hexagon is ______.
A rhombus is symmetrical about ______.
A kite has two lines of symmetry.
Find the number of lines of symmetry for the following shape:

Find the number of lines of symmetry for the following shape:

