Advertisements
Advertisements
Question
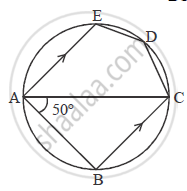
In the given figure, ABCDE is a pentagon inscribed in a circle such that AC is a diameter and side BC//AE.If
∠ BAC=50°, find giving reasons:
(i) ∠ACB
(ii) ∠EDC
(iii) ∠BEC
Hence prove that BE is also a diameter
Solution

Let ∠ACB be x, ∠EDC be y and ∠BEC as z.
Now, ∠ABC = 90° {Angle in a semi-circle}
(i) ∴ In ΔABC, ∠ABC + ∠BAC + ∠ACB = 180°
⇒ 90° + 50° + ∠ACB = 180°
∠ACB = 40° = x
(ii) Now, ∠EAC = ∠ACB {Alternate interior angles ∴ AC is transversal to the parallel lines AE & BC}
∴ ∠EAC = 40°
Also, ∠EAC + ∠EDC = 180°
∴ 40° + ∠EDC = 180°
⇒ ∠EDC = 140° = y
(iii) ∠EBC + ∠EDC = 180° {Angles in cyclic quadrilateral}
∠EBC + 140° = 180°
∠EBC = 40°
∴ In ΔEBC
∠BEC + ∠ECB + ∠EBC = 180°
∴ ∠BEC + 90° + 40° = 180°
∴ ∠BEC = 50°
Also in ΔEAB
∠EAB = ∠EAC + ∠BAC
= 40° + 50°
∠EAB = 90°
We know, if an angle of a triangle in a circle is 90o then, the hypotenuse must be the diameter of the circle. Hence, BE is the diameter of the circle.
APPEARS IN
RELATED QUESTIONS
Use graph paper to answer the following questions. (Take 2 cm = 1 unit on both axes)
1) Plot the points A( -4, 2) and B(2, 4)
2) A' is the image of A when reflected at the y-axis. Plot it on the graph paper and write the coordinates of A'.
3) B' is the image of B when reflected on the line AA'. Write the coordinates of B'.
4) Write the geometric name of the figure ABA'B'.
5) Name a line of symmetry of the figure formed
Draw an equilateral triangle each of whose side is 4 cm. Draw all its lines of symmetry.
Draw and answer the following.
A triangle which has no line of symmetry
The number of lines of symmetry in a ruler is ______.
The number of lines of symmetry in a 30° – 60° – 90° set square is ______.
A square and a rectangle have the same number of lines of symmetry.
A circle has only 16 lines of symmetry.
Find the number of lines of symmetry for the following shape:

Copy the triangle in the following figure on squared paper. Draw the line(s) of symmetry, if any and identify the type of triangle. (Some of you may like to trace the figure and try paper-folding first!)
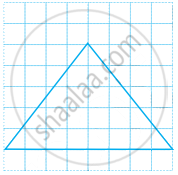
Can you draw a triangle which has exactly two lines of symmetry?
