Advertisements
Advertisements
प्रश्न
A 5⋅0 µF capacitor is charged to 12 V. The positive plate of this capacitor is now connected to the negative terminal of a 12 V battery and vice versa. Calculate the heat developed in the connecting wires.
उत्तर
As a capacitor of capacitance C is connected to the battery of voltage V, one of its plates gets charged to Q = CV and the other gets charged to −Q coulomb. When the polarity is reversed, charge −Q appears on the first plate and charge +Q appears on the second plate. So to maintain these charges, charge 2Q passes through the battery from the negative terminal to the positive terminal.
The work done by the battery is given by `W = 2QV = 2CE^2`
In the given process, the capacitor's energy remains the same in both cases. The work done by the battery appears as heat in the connecting wires.
Now,
Heat produced :
`H = 2CE^2`
`H = 2 xx (5 xx 10^-6) xx 144`
`H = 144 xx 10^-5 "J"= 1.44 "mJ"`
APPEARS IN
संबंधित प्रश्न
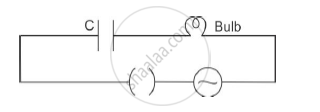
A bulb is connected in series with a variable capacitor and an AC source as shown. What happens to the brightness of the bulb when the key is plugged in and capacitance of the capacitor is gradually reduced?
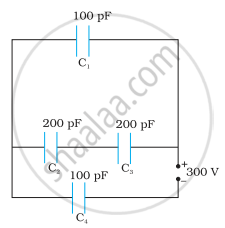
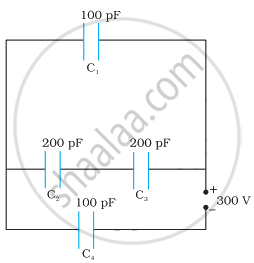
Obtain the equivalent capacitance of the network in Figure. For a 300 V supply, determine the charge and voltage across each capacitor.
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of a spherical capacitor is given by
C = `(4piin_0"r"_1"r"_2)/("r"_1 - "r"_2)`

where r1 and r2 are the radii of outer and inner spheres, respectively.
A capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
When 1⋅0 × 1012 electrons are transferred from one conductor to another, a potential difference of 10 V appears between the conductors. Calculate the capacitance of the two-conductor system.
Find the capacitance of the combination shown in figure between A and B.

Suppose the space between the two inner shells is filled with a dielectric of dielectric constant K. Find the capacitance of the system between A and B.
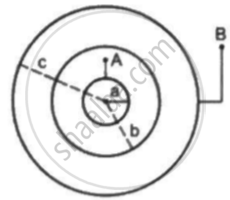
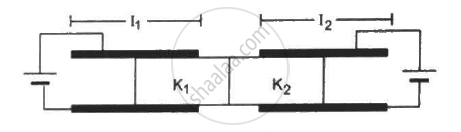
Figure shows two parallel plate capacitors with fixed plates and connected to two batteries. The separation between the plates is the same for the two capacitors. The plates are rectangular in shape with width b and lengths l1 and l2. The left half of the dielectric slab has a dielectric constant K1 and the right half K2. Neglecting any friction, find the ration of the emf of the left battery to that of the right battery for which the dielectric slab may remain in equilibrium.
Obtain the expression for capacitance for a parallel plate capacitor.
Obtain the expression for energy stored in the parallel plate capacitor.
Derive the expression for resultant capacitance, when the capacitor is connected in parallel.
Dielectric constant for a metal is ______.
When air is replaced by a dielectric medium of constant K, the maximum force of attraction between two charges separated by a distance ______.
For changing the capacitance of a given parallel plate capacitor, a dielectric material of dielectric constant K is used, which has the same area as the plates of the capacitor.
The thickness of the dielectric slab is `3/4`d, where 'd' is the separation between the plate of the parallel plate capacitor.
The new capacitance (C') in terms of the original capacitance (C0) is given by the following relation:
A leaky parallel plate capacitor is filled completely with a material having dielectric constant K = 5 and electric conductivity σ = 7.4 × 10-12 Ω-1 m-1. If the charge on the plate at the instant t = 0 is q = 8.85 µC, then the leakage current at the instant t = 12 s is ______ × 10-1 µA.
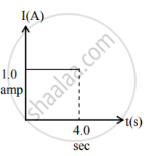
Current versus time and voltage versus time graphs of a circuit element are shown in figure.
 |
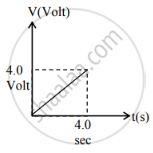 |
The type of the circuit element is ______.
A capacitor with capacitance 5µF is charged to 5 µC. If the plates are pulled apart to reduce the capacitance to 2 µF, how much work is done?
Obtain the equivalent capacitance of the network shown in the figure. For a 300 V supply, determine the charge on each capacitor.