Advertisements
Advertisements
प्रश्न
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD.
Prove that: ∠BCD = 90°
उत्तर
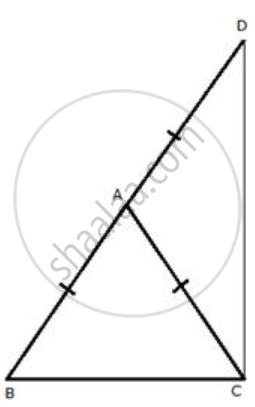
Const: Join CD.
In ΔABC,
AB = AC .........[ Given ]
∴ ∠C = ∠B .......(i) [angles opp. to equal sides are equal]
In ΔACD,
AC= AD ...[Given]
∴ ∠ADC = ∠ACD ........(ii)
Adding (i) and (ii)
∠B + ∠ADC = ∠C + ACD
∠B + ∠ADC = ∠BCD ....(iii)
In ΔBCD,
∠B + ∠ADC + ∠BCD = 180°
∠BCD + ∠BCD = 180° .......[From (iii)]
2∠BCD = 180°
∠BCD = 90°
APPEARS IN
संबंधित प्रश्न
In the figure given below, LM = LN; angle PLN = 110o.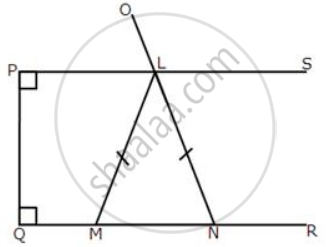
calculate: (i) ∠LMN
(ii) ∠MLN
In the figure, given below, AB = AC.
Prove that: ∠BOC = ∠ACD.

Calculate x :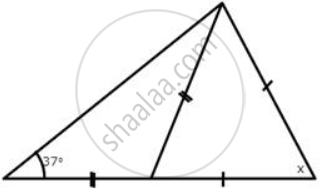
In the given figure; AB = BC and AD = EC.
Prove that: BD = BE.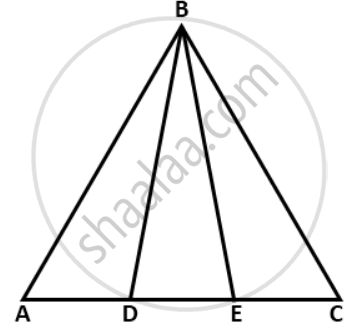
Prove that a triangle ABC is isosceles, if: altitude AD bisects angles BAC.
In the given figure, AD = AB = AC, BD is parallel to CA and angle ACB = 65°. Find angle DAC.
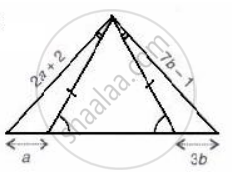
Using the information given of the following figure, find the values of a and b.
Use the given figure to prove that, AB = AC.
Prove that the medians corresponding to equal sides of an isosceles triangle are equal.
The bisectors of the equal angles B and C of an isosceles triangle ABC meet at O. Prove that AO bisects angle A.
