Advertisements
Advertisements
प्रश्न
In a parallelogram ABCD, if ∠A = (3x − 20)°, ∠B = (y + 15)°, ∠C = (x + 40)°, then find the values of xand y.
उत्तर
In parallelogram ABCD, ∠A and ∠C are opposite angles.
We know that in a parallelogram, the opposite angles are equal.
Therefore,
∠C = ∠A
We have ∠A = (3x - 20°) and ∠C = (x + 40°)
Therefore,
x + 40° = 3x - 20°
x - 3x = -40° - 20°
-2x = - 60°
x = 30°
Therefore,
∠A = (3x - 20°)
∠A = [3(30) - 20°]
∠A = 70°
Similarly,
∠C = 70°
Also, ∠B = ( y + 15)°
Therefore,
∠D = ∠B
∠D = (y + 15 )°
By angle sum property of a quadrilateral, we have:
∠A + ∠B + ∠C + ∠D = 360°
70° +(y + 15)° + 70° + (y + 15)° = 360°
140° + 2 (y + 15)° = 360°
2(Y + 15)° = 360° - 140°
2(y + 15)° = 220°
(y + 15)° = 110°
y = 95°
Hence the required values for x and y are 30° and 95° respectively.
APPEARS IN
संबंधित प्रश्न
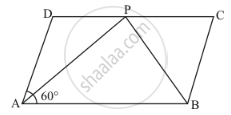
In Fig., below, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.
In a parallelogram ABCD, if `∠`B = 135°, determine the measures of its other angles .
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a
parallelogram.
In a parallelogram ABCD, write the sum of angles A and B.
In a parallelogram ABCD, if ∠D = 115°, then write the measure of ∠A.
PQRS is a quadrilateral, PR and QS intersect each other at O. In which of the following case, PQRS is a parallelogram?
∠P = 100°, ∠Q = 80°, ∠R = 95°
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
In the given Figure, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF. (Use congruent property of triangles)
Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
