Advertisements
Advertisements
प्रश्न
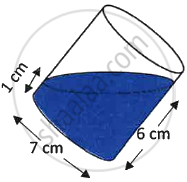
In the adjoining diagram, a tilted right circular cylindrical vessel with base diameter 7 cm contains a liquid. When placed vertically, the height of the liquid in the vessel is the mean of two heights shown in the diagram. Find the area of wet surface, when the cylinder is placed vertically on a horizontal surface. (Use π = `22/7`).
उत्तर
The cylinder has a base diameter of 7 cm, so the radius r is:
r = `7/2 = 3.5 " cm"`
The heights of the liquid when tilted are h1 = 1 and h2 = 6 cm.
∴ h = `(h_1 + h_2)/2`
`\implies` h = `1/2(1 + 6)`,
`\implies` h = `7/2`
`\implies` h = 3.5 cm
Area of wet surface = πr2 + 2πrh
Area of base = πr2
= `22/7 xx (3.5)^2`
= 38.5 cm2
Lateral surface area = 2πrh
= `2 xx 22/7 xx 3.5 xx 3.5`
= `2 xx 22/7 xx 12.25`
= 77 cm2
Total wet surface area = Area of base + Lateral area
= 38.5 cm2 + 77 cm2
= 115.5 cm2
APPEARS IN
संबंधित प्रश्न
The total surface area of a hollow metal cylinder, open at both ends of external radius 8 cm and height 10 cm is 338 p `cm^2`. Taking r to be inner radius, obtain an equation in r and use it to obtain the thickness of the metal in the cylinder.
The diameter of the base of a right circular cylinder is 42 cm and its height is 10 cm. Find the volume of the cylinder.
The volume and the curved surface area of a cylinder are 1650 cm3 and 660 cm2respectively. Find the radius and height of the cylinder.
How many cubic metres of earth must be dug-out to sink a well 21 m deep and 6 m diameter?
Two circular cylinders of equal volumes have their heights in the ratio 1 : 2. Find the ratio of their radii.
If the radius of a cylinder is doubled and the height remains same, the volume will be
If the height of a cylinder is doubled and radius remains the same, then volume will be
The curved surface area of a cylinder is 198cm2 and its base has diameter 21cm. Find the height and the volume of the cylinder.
The difference between the outer and inner curved surface area of a hollow cylinder is 264 cm2. If its height is 14 cm and the volume of the material in it is 1980 cm3, find its total surface area.
In the example given below, the radius of the base of a cylinder and its height is given. Then find the curved surface area and total surface area.
r = 1.4 cm, h = 2.1 cm
