Advertisements
Advertisements
प्रश्न
जर ΔABC ~ ΔDEF आणि ∠A = 45°, ∠E = 35° असल्यास ∠B चे माप किती?
पर्याय
45°
35°
25°
40°
उत्तर
35°
APPEARS IN
संबंधित प्रश्न
दोन समरूप त्रिकोणांच्या संगत बाजूंचे गुणोत्तर 3 : 5 आहे, तर त्यांच्या क्षेत्रफळांचे गुणोत्तर काढा.
Δ ABC व Δ DEF हे दोन्ही समभुज त्रिकोण आहेत. A (ΔABC) : A (Δ DEF) = 1 : 2 असून AB = 4 तर DE ची लांबी काढा.
ΔABC व ΔDEF मध्ये ∠B = ∠E, ∠F = ∠C आणि AB = 3 DE, तर त्या दोन त्रिकोणांबाबत सत्य विधान कोणते?
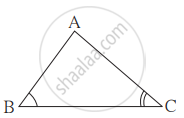
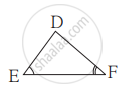
ΔABC व ΔDEF हे दोन्ही समभुज त्रिकोण आहेत, A(ΔABC) : A(ΔDEF) = 1 : 2 असून AB = 4 आहे तर DE ची लांबी किती?
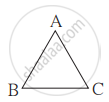
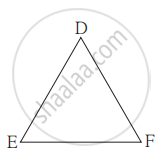
जर ∆ABC ~ ∆LMN आणि ∠A = 60° असल्यास ∠L = ?
∆ABC ~ ∆LMN आणि ∠B = 40° तर ∠M चे माप किती? कारण लिहा.
∆ABP ~ ∆DEF आणि A(∆ABP) : A(∆DEF) = 144:81 तर AB:DE = ?
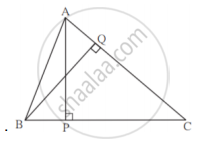
∆ABC मध्ये, AP लंब BC व BQ लंब AC, B-P-C, A-Q-C, तर ∆CPA ~ ∆CQB दाखवा. जर AP = 7, BQ = 8, BC = 12 असल्यास AC ची किंमत काढा.
∆CPA व ∆CQB मध्ये,
∠CPA ≅ `square` ...........[प्रत्येकी 90°]
∠ACP ≅ `square` ...........[सामाईक कोन]
∆CPA ~ ∆CQB ............[`square` समरूपता कसोटी]
`"AP"/"BQ" = square/"BC"` ............…[समरूप त्रिकोणांच्या संगत बाजू प्रमाणात]
`7/8 = square/12`
AC × `square` = 7 × 12
AC = 10.5
दोन समरूप त्रिकोणांची क्षेत्रफळे समान असल्यास ते त्रिकोण एकरूप असतात. सिद्ध करा.
ΔABC मध्ये रेख DE || बाजू BC. जर 2A(ΔADE) = A(⬜ DBCE), तर AB : AD आणि BC = `sqrt3` DE दाखवा.
