Advertisements
Advertisements
प्रश्न
किसी समांतर चतुर्भुज की दो संलग्न भुजाओं के वर्गों का योगफल 130 वर्ग सेमी हो तथा उसके एक विकर्ण की लंबाई 14 सेमी हो तो उसके दूसरे विकर्ण की लंबाई ज्ञात कीजिए।
उत्तर
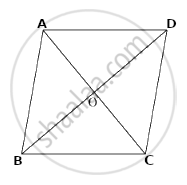
मानो कि, `square`ABCD एक दिया गया चतुर्भुज है, जिसमें विकर्ण AC तथा विकर्ण BD परस्पर बिंदु O पर प्रतिच्छेदित करते है |
AB2 + BC2 = 130 सेमी और AC = 14 सेमी
AO = `1/2`AC ...............(समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते है)
∴ AO = `1/2`AC
∴ AO = 7 सेमी
ΔABC में, रेख BO माध्यिका है ........... (परिभाषा से)
∴ अपोलोनियस के प्रमेय से,
AB2 + BC2 = 2BO2 + 2AO2
∴ 130 = 2BO2 + 2(7)2
∴ 130 = 2BO2 + 2 × 49
∴ 130 = 2BO2 + 98
∴ 2BO2 = 130 - 98
∴ 2BO2 = 32
∴ BO2 = `32/2`
∴ O2 = 16
∴ BO = 4 सेमी ................(दोनों पक्षों का वर्गमूल लेने पर)
BO = `1/2`BD ...............(समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते है |)
∴ 4 = `1/2`BD
BD = 8 सेमी
समांतर चतुर्भुज के दूसरे विकर्ण की लंबाई 8 सेमी है |
APPEARS IN
संबंधित प्रश्न
ΔPQR में, बिंदु S यह भुजा QR का मध्यबिंदु है, यदि PQ = 11, PR = 17, PS = 13 हो तो QR की लंबाई ज्ञात कीजिए।
ΔABC में, AB = 10, AC = 7, BC = 9 तो बिंदु C से भुजा AB पर खींची गई माध्यिका की लंबाई कितनी होगी?
आकृति में, ΔABC में बिंदु M यह भुजा BC का मध्यबिंदु है, यदि AB2 + AC2 = 290 सेमी, AM = 8 सेमी, तो BC ज्ञात कीजिए।
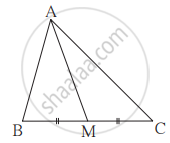
ΔABC में रेख AP माध्यिका है। यदि BC = 18, AB2 + AC2 = 260 तो AP ज्ञात कीजिए।
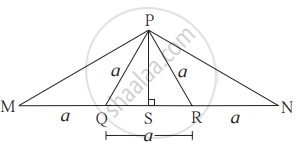
आकृति में M-Q-R-N दी गई जानकारी के आधार पर सिद्ध कीजिए कि : PM = PN = `sqrt3 xx a`
सिद्ध कीजिए कि, समांतर चतुर्भुज के विकर्णों के वर्गों का योगफल उस चतुर्भुज की भुजाओं के वर्गों के योगफल के बराबर होता है।
ΔPQR में रेख PM यह माध्यिका है। यदि PQ = 40, PR = 42 और PM = 29, तो QR की लंबाई ज्ञात कीजिए।
ΔABC में रेख AM यह माध्यिका है। यदि AB = 22, AC = 34, BC = 24, तो AM की लंबाई ज्ञात कीजिए।
ΔPQR में, रेख PM माध्यिका है PM = 9 और PQ2 + PR2 = 290 हो, तो QR ज्ञात कीजिए।
