Advertisements
Advertisements
प्रश्न
क्या भुजा a cm वाले वर्ग के अंतर्गत खींचे गये वृत्त का क्षेत्रफल πa2 cm2 होता है? अपने उत्तर के लिए कारण दीजिए।
उत्तर
मान लीजिए a वर्ग की भुजा है।
हमें दिया गया है कि वृत्त वर्ग में अंकित है।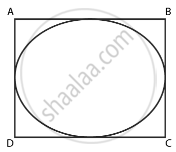
वृत्त का व्यास = वर्ग की भुजा = a
वृत्त की त्रिज्या = `"a"/2`
वृत्त का क्षेत्रफल = πr2
= `π("a"/2)^2`
= `(π"a"^2)/4` cm2
अतः, वृत्त का क्षेत्रफल `(π"a"^2)/4` cm2 है।
इस प्रकार एक सेमी भुजा वाले वर्ग में अंकित वृत्त का क्षेत्रफल a2 cm2 नहीं है।
APPEARS IN
संबंधित प्रश्न
दो वृत्तों की त्रिज्याएँ क्रमश: 8 सेमी और 6 सेमी हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के बराबर है।
किसी कार के प्रत्येक पहिए का व्यास 80 सेमी है। यदि यह कार 66 किमी प्रति घंटे की चाल से चल रही है, तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाती है?
[इस्तेमाल करें Π = 22/7]
जहाजों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए, एक लाइट हाउस 80 डिग्री कोण वाले एक त्रिज्यखंड में 16.5 किमी की दूरी तक लाल रंग का प्रकाश फैलाता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाज को चेतावनी दी जा सके। [उपयोग π = 3.14]
त्रिज्या के एक अर्धवृत्त के अंतर्गत खींचे जा सकने वाले सबसे बड़े त्रिभुज का क्षेत्रफल ______ है।
यदि एक वृत्त का परिमाप एक वर्ग के परिमाप के बराबर है, तो उनके क्षेत्रफलों का अनुपात ______ है।
भुजा 6 cm वाले एक वर्ग के अंतर्गत खीचे जा सकने वाले वृत्त का क्षेत्रफल ______ है।
त्रिज्याओं 24 cm और 7 cm वाले दो वृत्तों के क्षेत्रफलों के योग के बराबर क्षेत्रफल वाले एक वृत्त का व्यास ______ है।
क्या यह कहना सत्य होगा कि त्रिज्या a cm वाले एक वृत्त के परिगत वर्ग का परिमाप 8 cm है? अपने उत्तर का कारण दीजिए।
क्या लंबाई a cm और चौड़ाई b cm (a > b) वाले एक आयत के अंदर खींचे जा सकने वाले सबसे बड़े वृत्त का क्षेत्रफल πb2 cm2 है? क्यों?
आकृति में, विकर्ण 8 cm वाला एक वर्ग एक वृत्त के अंतर्गत है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

