Advertisements
Advertisements
प्रश्न
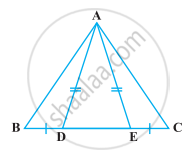
निम्नलिखित आकृति में, D और E त्रिभुज ABC की भुजा BC पर दो बिंदु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। दर्शाइए कि ∆ABD ≅ ∆ACE है।
उत्तर
दिया गया है - एक ∆ABC की भुजा BC पर बिंदु D और E इस प्रकार हैं कि BD = CE और AD = AE है।
दर्शाना है - ∆ABD ≅ ∆ACE
उपपत्ति - हमारे पास, AD = AE ...[दिया गया है।]
⇒ ∠ADE = ∠AED ...(i) [चूँकि, समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
हमारे पास है, ∠ADB + ∠ADE = 180° ...[रैखिक युग्म अभिगृहीत]
⇒ ∠ADB = 180° – ∠ADE
= 180° – ∠AED ...[समीकरण (i) से]
∆ABD और ∆ACE में,
∠ADB = ∠AEC ...[∵ ∠AEC + ∠AED = 180°, रैखिक युग्म अभिगृहीत]
BD = CE ...[दिया गया है।]
और AD = AE ...[दिया गया है।]
∴ ∆ABD ≅ ∆ACE ...[SAS सर्वांगसमता नियम द्वारा]
APPEARS IN
संबंधित प्रश्न
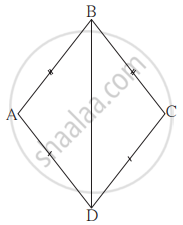
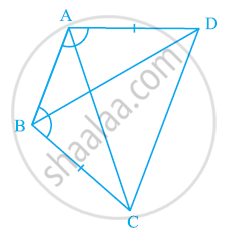
ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB = ∠CBA है (देखिए आकृति)। सिद्ध कीजिए कि:
- △ABD ≌ △BAC
- BD = AC
- ∠ABD = ∠BAC
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो `barEF` के संगत हो:
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो `bar(DF)` के संगत हो:
कथनों को पूरा कीजिए:
ΔBCA ≅?
∆QRS ≅ ?
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि त्रिभुज सर्वांगसम हों
आप उनके परिमाप के बारे में क्या कह सकते हैं?
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि त्रिभुज सर्वांगसम न हों।
आप उनके परिमाप के बारे में क्या कह सकते हैं?
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है
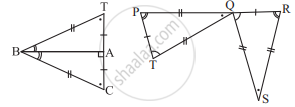
नीचे दिए गए प्रत्येक उदाहरण में त्रिभुज की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। प्रत्येक जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।

______ कसौटी से
ΔPRQ ≅ ΔSTU
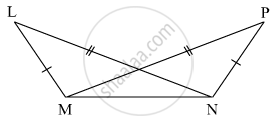
नीचे दी गई आकृति में दर्शाए अनुसार ΔLMN तथा ΔPNM में LM = PN, LN = PM हो तो त्रिभुजों की सर्वांगसमता की कसौटी लिखिए । शेष सर्वांगसम घटकों के नाम भी लिखिए ।
आकृति में रेख AB ≅ रेख BC तथा रेख AD ≅ रेख CD तो सिद्ध कीजिए Δ ABD ≅ Δ CBD