Advertisements
Advertisements
प्रश्न
Obtain an expression for the resultant amplitude of, the composition of two S.H.M.’s having the same period along the same path.
उत्तर
- Consider a particle simultaneously subjected to two S.H.M.s having the same period and along the same path (let it be along the x-axis) but of different amplitudes and initial phases. The resultant displacement at any instant is equal to the vector sum of its displacements due to both the S.H.M.s at that instant.
- Let the two linear S.H.M’s be given by equations,
x1 = A1 sin (ωt + Φ1) ....(1)
x2 = A2 sin (ωt + Φ2) ....(2)
where A1, A2 are amplitudes; Φ1, Φ2 are initial phase angles, and x1, x2 are the displacement of two S.H.M’s in time ‘t’. ω is the same for both S.H.M’s. - The resultant displacement of the two S.H.M’s is given by,
x = x1 + x2 ....(3)
Using equations (1) and (2) , equation (3) can be written as,
x = A1 sin (ωt + Φ1) + A2 sin (ωt + Φ2)
= A1 [sin ωt cos Φ1 + cos ωt sin Φ1] + A2 [sin ωt cos Φ2 + cos ωt sin Φ2]
= A1 sin ωt cos Φ1 + A1 cos ωt sin Φ1 +A2 sin ωt cos Φ2 + A2 cos ωt sin Φ2
= [A1 sin ωt cos Φ1 + A2 sin ωt cos Φ2] + [A1 cosωt sin Φ1 + A2 cos ωt sinΦ2]
∴ x = sin ωt [A1 cos Φ1 + A2 cos Φ2] + cos ωt [A1 sin Φ1 + A2 sin Φ2] .…(4) - As A1, A2, Φ1 and Φ2 are constants, we can combine them in terms of another convenient constants R and δ as
A1 cos Φ1 + A2 cos Φ2 = R cosδ .…(5)
and A1 sin Φ1 + A2 sin Φ2 = R sin δ .…(6) - Using equations (5) and (6), equation (4) can be written as,
x = sin ωt. R cos δ + cos ωt.R sin δ = R [sin ωt cos δ + cos ωt sin δ]
∴ x = R sin (ωt + δ) ....(7)
Equation (7) is the equation of an S.H.M. of the same angular frequency (hence, the same period) but of amplitude R and initial phase δ. It shows that the combination (superposition) of two linear S.H.M.s of the same period and occurring along the same path is also an S.H.M. - Resultant amplitude is,
R = `sqrt(("R" sinδ)^2 + ("R" cosδ)^2)`
Squaring and adding equations (5) and (6) we get, (A1 cos Φ1 + A2 cos Φ2)2 + (A1 sin Φ1 + A2 sin Φ2)2 = R2 cos2 δ + R2 sin2 δ
∴ `A_1^2 cos^2 Φ_1 + A_2^2 cos^2 Φ_2 + 2A_1 A_2 cos Φ_1 cosΦ_2 + A_1^2 sin^2 Φ_1 + A_2^2 sin^2 Φ_2 + 2A_1A_2 sinΦ_1 sinΦ_2 = R^2 (cos^2 δ + sin^2 δ)`
∴ `A_1^2 (cos^2 Φ_1 + sin^2 Φ_1) + A_2^2 (cos^2 Φ_2 + sin^2 Φ_2) + 2A_1A_2 (cos Φ_1 cos Φ_2 + sinΦ_1 sinΦ_2) = R^2`
∴ `A_1^2 + A_2^2 + 2A_1A_2 cos (Φ_1 − Φ_2) = R^2`
∴ R = ± `sqrt(A_1^2 + A_2^2 + 2A_1A_2cos(Φ_1 − Φ_2))` ....(8)
Equation (8) represents resultant amplitude of two S.H.M’s.
संबंधित प्रश्न
A needle of a sewing machine moves along a path of amplitude 4 cm with a frequency of 5 Hz. Find its acceleration `(1/30)` s after it has crossed the mean position.
Potential energy of a particle performing linear S.H.M. is 0.1 π2x2 joule. If the mass of the particle is 20 g, find the frequency of S.H.M.
Two S.H.M.’s have zero phase difference and equal amplitudes A. The resultant amplitude on their composition will be ______
A simple pendulum moves from one end to the other in ¼ second. What is its frequency?
What is the amplitude of S.H.M.
The acceleration due to gravity on the surface of the moon is 1.7 m/s2. What is the time period of a simple pendulum on the surface of the moon if its time period on the surface of the earth is 3.5 s? (g on the surface of earth = 9.8 m/s2)
A particle performs linear S.H.M. of period 4 seconds and amplitude 4 cm. Find the time taken by it to travel a distance of 1 cm from the positive extreme position.
Two wires of different materials have same length L and same diameter d. The second wire is connected at the end of the first wire and forms one single wire of double the length. This wire is subjected to stretching force F to produce the elongation l. The two wires have ______.
The total energy of the body executing S.H.M. is E. The kinetic energy of the body, when the displacement is half of the amplitude is ______.
When a mass is hung from a light spring, the spring extends by 10 cm. If the mass is pulled down and let go, it executes S.H.M. with a time period (g = 10 m/s2) ____________.
A particle is executing S.H.M. with amplitude of 4 cm and time period 12 s. The time taken by the particle in going from its mean position to a position of displacement equal to 2 cm is T1 The time taken from this displaced position of 2 cm to reach the extreme position is T2. T1/ T2 will be____________.
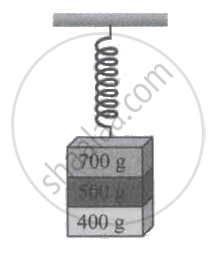
Three masses 700 g, 500 g, and 400 g are suspended at the end of a spring and are in equilibrium as shown in figure. When the 700 g mass is removed, the system oscillates with a period of 3 seconds; when the 500 g mass is also removed, it will oscillate with a period of ____________.
The equation of S.H.M. of a particle of amplitude 4 cm performing 150 oscillations per minute starting with an initial phase 30° is ____________.
The amplitude of sound is doubled and the frequency is reduced to one fourth. The intensity of sound at the same point will be ____________.
A body of mass 1 kg is suspended from a spring of negligible mass. Another body of mass 500 g moving vertically upwards hits the suspended body with a velocity 3 ms-1 and gets embedded in it. If the frequency of oscillation of the system of the two bodies after collision `10/pi` Hz, the amplitude of motion and the spring constant are respectively ____________.
A horizontal spring executes S.H.M. with amplitude 'A1', when mass 'm1' is attached to it, When it passes through mean position another mass 'm2' is placed on it. Both masses move together with amplitude 'A2'. Therefore A2 : A1 is ______
A mass M attached to a horizontal spring executes S.H.M. of amplitude A1. When the mass M passes through its mean position, then a smaller mass m is placed over it and both of them move together with amplitude A2. The ratio of `(A_1/A_2)` is ______
Two trains are moving towards each other with speeds of 20m/s and 15 m/s relative to the ground. The first train sounds a whistle of frequency 600 Hz. The frequency of the whistle heard by a passenger in the second train before the train meets, is ______. (the speed of sound in air is 340 m/s)
A mass m1 connected to a horizontal spring performs SHM with amplitude A. While mass m1 is passing through mean position, another mass m2 is placed on it so that both the masses move together with amplitude A1. The ratio of `"A"_1/"A"` is ______. (m2 < m1)
A sinusoidal wave travelling in the same direction have amplitudes of 3 cm and 4 cm and difference in phase by `pi/2`. The resultant amplitude of the superimposed wave is ______.
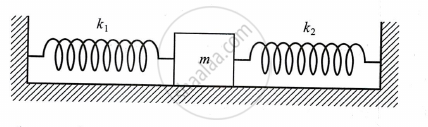
A block of mass m, connected to two springs of spring constants k1 and k2 as shown, oscillates on a smooth horizontal surface. What is the effective spring constant of the oscillation?
Light of a certain colour has 2500 waves to the millimetre in air. What is its frequency?
