Advertisements
Advertisements
प्रश्न
Obtain an expression for the torque acting on a rotating body with constant angular acceleration. Hence state the dimensions and SI unit of torque.
Obtain an expression for the torque acting on a rotating body with constant angular acceleration.
उत्तर
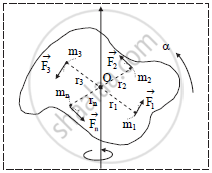
For m1, a1 = r1α
For m2, a2 = r2α
For mn, an = rnα
f1 = m1a1 = m1r1α
f2 = m2a2 = m2r2α
fn = mnrnα
Torque `(vectau) = vecr xx vecf`
= rfsin90°
τ = rf
`tau_1 = "r""f"_1 = "m"_1"r"_1^2alpha`
`tau_2 = "m"_2"r"_2^2alpha`
`tau_"n" = "m"_"n""r"_"n"^2alpha`
`tau = tau_1 + tau_2 + ... + tau_n`
Total Torgue on the body, `vectau_"net" = vectau_1 + vectau_2 + vectau_3 + ... vectau_"n"`
= `"m"_1"r"_1^2alpha + "m"_2"r"_2^2alpha + ..... + "m"_"n""r"_"n"^2alpha`
= `alpha("m"_1"r"_1^2 + "m"_2"r"_2^2 + ..... + "m"_"n""r"_"n"^2)`
I = mr2
`vectau_"net" = ("I"_1 + "I"_2 + "I"_3 + ......"I"_n)alpha`
= `"I"alpha`
Unit: N.m
dimension: [ML2T-2]
APPEARS IN
संबंधित प्रश्न
Obtain an expression for torque acting on a body rotating with uniform angular acceleration.
An electron(e) is revolving in a circular orbit of radius r in the hydrogen atom. The angular momentum of the electron is (M = magnetic dipole moment associated with it and m = mass of electron)
A stone of mass 1 kg is rotated in a horizontal circle of radius 0.5 m. If it makes `100/pi` rps, then its angular momentum is ______
A charged particle (charge = q: mass = m) is rotating in a circle of radius 'R' with uniform speed 'v'. The ratio of its magnetic moment (M) to the angular momentum (L) is ______
Angular momentum of the earth revolving around the sun is proportional to rn , where r is the distance between the earth and the sun. Value of n is ____________.
If the angular momentum of a body increases by 50%, then its kinetic energy of rotation increases by ______ (M.I. remains constant)
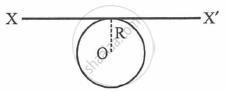
A thin metal wire of length 'L' and uniform linear mass density 'ρ' is bent into a circular coil with 'O' as centre. The moment of inertia of a coil about the axis XX' is ______.
If the kinetic energy of rotation of a body is doubled, then its angular momentum ____________.
A particle of mass m is rotating in a plane in a circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is ______.
A homogeneous disc of mass 2 kg and radius 15 cm is rotating about its axis (which is fixed) with an angular velocity of 4 radian/s. The linear momentum of the disc is ____________.
Let I1 and I2 be the moments of inertia of two bodies of identical geometrical shape. If the first body is made of aluminium and the second of iron, then ____________.
Earth revolves round the sun in a circular orbit of radius 'R'. The angular momentum of the revolving earth is directly proprtional to ______.
An electron has a mass of 9.1 x 10-31 kg. It revolves round the nucleus in a circular orbit of radius 0.529 x 10-10 metre at a speed of 2.2 x 106 m/s. The magnitude of its linear momentum in this motion is ____________.
The direction of angular momentum of particle is ____________.
An electron of mass 'm' revolving around the nucleus in a circular orbit of radius 'r' has angular momentum 'L'. The magnetic field produced by the electron at the centre of the orbit is e = electric charge, µ0 = permeability of free space ____________.
A particle is revolving in anticlockwise sense along the circumference of a circle of radius 'r' with linear velocity 'v', then the angle between 'v' and angular velocity 'ω' will be ______.
An electron in an atom is revolving round the nucleus in a circular orbit of radius 5.3 × 10-11 m with a speed of 3 × 106 m/s. Find the angular momentum of electron.
A wheel of moment of inertia 2 kg m2 is rotating about an axis passing through centre and perpendicular to its plane at a speed 60 rad/s. Due to friction, it comes to rest in 5 minutes. The angular momentum of the wheel three minutes before it stops rotating is ______.
A disc of moment of inertia 'I1' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'ω1'. Another disc of moment of inertia 'I2' having zero angular speed is placed co-axially on a rotating disc. Now, both the discs are rotating with constant angular speed 'ω2'. The energy lost by the initial rotating disc is ______.
Define angular momentum.
Calculate the change in angular momentum of the electron when it jumps from third orbit to first orbit in hydrogen atom.
(Take h = 6.33 × 10−34 Js)
