Advertisements
Advertisements
प्रश्न
Obtain the conditions for the bright and dark fringes in diffraction pattern due to a single narrow slit illuminated by a monochromatic source.
Explain clearly why the secondary maxima go on becoming weaker with increasing.
उत्तर

Consider a point P on the screen at which wavelets travelling in a direction making angle θ with CO are brought to focus by the lens. The wavelets from points A and B will have a path difference equal to BN.
From the right-angled ΔANB, we have
BN = AB sinθ
BN = a sinθ …(1)
Suppose BN = λ and θ = θ1
Then, the above equation gives
λ = a sin θ1
`sin theta_1 = lambda/a ........ (2)`
Such a point on the screen will be the position of first secondary minimum.
If BN = 2λ and θ= θ2, then
2λ = a sin θ2
`sin theta_2 = (2lambda)/a .......... (3)`
Such a point on the screen will be the position of second secondary minimum. In general, for nth minimum at point P,
`sintheta_n = (nlambda)/a ........ (4)`
If yn is the distance of the nth minimum from the centre of the screen, then from right-angled ΔCOP, we have
`tantheta_n =(OP)/(CO)=y_n/D .............. (5)`
In case θn is small, sin θn ≈ tan θn
∴ Equations (iv) and (v) give
`(y_n)/D = (nlambda)/a`
`y_n = (nlambdaD)/a`
If `BN = (3lambda)/2`and θ = θ1′, then from equation (i), we have
`sintheta_1^' = (3lambda)/(2a)`
Such a point on the screen will be the position of the first secondary maximum. Corresponding to path difference,
`BN =(5lambda)/2`and θ = θ ′2, the second secondary maximum is produced
In general, for the nth maximum at point P,
`sintheta_n^' = ((2n+1)lambda)/(2a) .............. (6)`
If is the distance of nth maximum from the centre of the screen, then the angular position of the nth maximum is given by,
`tantheta_n^' = (y_n)/a ....... (7)`
In case θ′n is small,
sin θ’n ≈ tan θ’n
`y_n^' = ((2n+1)lambdaD)/(2a)`
For n = 1,
`theta' = (3lambda)/(2a)`(From eq(6), small angle approximation, `sin theta' =theta' = ((2n+1)lambda)/(2a)`
This angle is midway between two of the dark fringes. Divide the slit into three equal parts. If we take the first two third part of the slit the path difference between the two ends would be,
`2/3 a xx theta' = lambda`
The first two third is divided into two halves which have path difference `lambda/2`. The contribution due to these two halves is 180° out of phase and gets cancel. Only the remaining one third part of the slit contributes to the intensity at a point between the two minima which will be much weaker than the central maxima. Thus with increasing n the intensity of maxima gets weaker.
संबंधित प्रश्न
When light travels from a rarer to a denser medium, the speed decreases. Does this decrease in speed imply a reduction in the energy carried by the wave?
In the wave picture of light, the intensity of light is determined by the square of the amplitude of the wave. What determines the intensity in the photon picture of light?
A monochromatic ray of light falls on a regular prism. What is the relation between the angle of incidence and angle of emergence in the case of minimum deviation?
State Huygen’s principle. Using this principle explain how a diffraction pattern is obtained on a screen due to a narrow slit on which a narrow beam coming from a `=> n = (vlamda)/(vlamda_omega)`monochromatic source of light is incident normally.
Can the interference pattern be produced by two independent monochromatic sources of light? Explain.
Find the angle of incidence at which a ray of monochromatic light should be incident on the first surface AB of a regular glass prism ABC so that the emergent ray grazes the adjacent surface AC. (Refractive Index of glass = 1 .56)
Answer the following question.
In the diffraction due to a single slit experiment, the aperture of the slit is 3 mm. If monochromatic light of wavelength 620 nm is incident normally on the slit, calculate the separation between the first order minima and the 3rd order maxima on one side of the screen. The distance between the slit and the screen is 1.5 m.
(a) Can the interference pattern be produced by two independent monochromatic sources of light? Explain.
(b) The intensity at the central maximum (O) in Young's double-slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would `"I"_°/4`
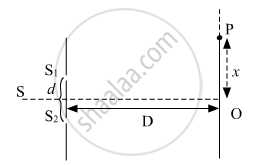
(c) In Young's double-slit experiment, the slits are separated by 0⋅5 mm and the screen is placed 1⋅0 m away from the slit. It is found that the 5th bright fringe is at a distance of 4⋅13 mm from the 2nd dark fringe. Find the wavelength of light used.
A monochromatic ray of light falls on a regular prism under minimum deviation condition. What is the relation between angle of incidence and angle of emergence?
Monochromatic light of wavelength 600 nm is incident from the air on a water surface. The refractive index of water is 1.33. Find the
- wavelength,
- frequency and
- speed, of reflected and refracted light.
