Advertisements
Advertisements
प्रश्न
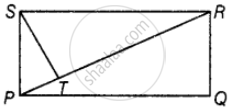
PQRS एक आयत है। S से PR पर डाला गया लंब ST कोण S को 2:3 के अनुपात में विभाजित करता है। ∠TPQ को ज्ञात कीजिए।
उत्तर
दिया गया है, ST ⊥ PR और ST, ∠S को 2:3 के अनुपात में विभाजित करते हैं।
इसलिए, अनुपात का योग = 2 + 3 = 5
अब, `∠TSP = 2/5 xx 90^circ = 36°, ∠TSR = 3/5 xx 90^circ = 54°`
साथ ही, त्रिभुज के कोणों के योग के गुण से,
∠TPS = 180° – (∠STP + ∠TSP)
= 180° – (90° + 36°)
= 54°
हम जानते हैं कि, ∠SPQ = 90°
⇒ ∠TPS + TPQ = 90°
⇒ 54° + ∠TPQ = 90°
⇒ ∠TPQ = 90° – 54° = 36°
APPEARS IN
संबंधित प्रश्न
एक सम अष्टभुज (regular octagon) का एक रफ़ चित्र खींचिए। [यदि आप चाहें, तो वर्गांकित कागज़ (squared paper) का प्रयोग कर सकते हैं।] इस अष्टभुज के चार शीर्षों को जोड़कर एक आयत खींचिए।
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
यदि किसी समांतर चतुर्भुज के आसन्न कोण बराबर हों, तो वह है एक –
आयत एक सम चतुर्भुज है।
यदि एक समचतुर्भुज के विकर्ण बराबर हों, तो वह अवश्य ही आयत होगा।
प्रत्येक समांतर चतुर्भुज एक आयत है।
चतुर्भुज EFGH एक आयत है, जिसमें J दोनों विकर्णों का प्रतिच्छेद बिंदु है। x का मान ज्ञात कीजिए, JF = 8x + 4 और EG = 24x − 8 है।
सिद्ध कीजिए कि, आयत एक समांतर चतुर्भुज होता है।
नीचे दिए गए कथन सत्य हैं या असत्य, कारण सहित लिखिए।
प्रत्येक समांतर चतुर्भुज, आयत होता है।
आयत PQRS के विकर्ण परस्पर बिंदु M पर प्रतिच्छेदित करते हैं। यदि `angle`QMR = 50° तो `angle`MPS का माप ज्ञात कीजिए।
