Advertisements
Advertisements
प्रश्न
PQRS एक आयत है। S से PR पर डाला गया लंब ST कोण S को 2:3 के अनुपात में विभाजित करता है। ∠TPQ को ज्ञात कीजिए।
उत्तर
दिया गया है, ST ⊥ PR और ST, ∠S को 2:3 के अनुपात में विभाजित करते हैं।
इसलिए, अनुपात का योग = 2 + 3 = 5
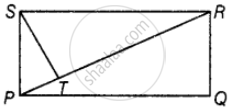
अब, `∠TSP = 2/5 xx 90^circ = 36°, ∠TSR = 3/5 xx 90^circ = 54°`
साथ ही, त्रिभुज के कोणों के योग के गुण से,
∠TPS = 180° – (∠STP + ∠TSP)
= 180° – (90° + 36°)
= 54°
हम जानते हैं कि, ∠SPQ = 90°
⇒ ∠TPS + TPQ = 90°
⇒ 54° + ∠TPQ = 90°
⇒ ∠TPQ = 90° – 54° = 36°
APPEARS IN
संबंधित प्रश्न
बताइए कैसे एक वर्ग एक आयत है।
बताइए एक आयत उत्तल चतुर्भुज कैसे है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग को एक विशेष प्रकार का आयत समझा जा सकता है।
निम्न में से किस के लिए, सभी कोण बराबर होते हैं?
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
नीचे दिये आयत READ में, ∠EAR ,∠RAD और ∠ROD ज्ञात कीजिए।
नीचे दिये आयत PAIR में, ∠ARI, ∠RMI और ∠PMA ज्ञात कीजिए।
चतुर्भुज EFGH एक आयत है, जिसमें J दोनों विकर्णों का प्रतिच्छेद बिंदु है। x का मान ज्ञात कीजिए, JF = 8x + 4 और EG = 24x − 8 है।
रेखा l रेखा m के समांतर है तथा एक तिर्यक रेखा p क्रमशः इन्हें X और Y पर प्रतिच्छेद करती है। X और Y पर स्थित अंतःकोणों के समद्विभाजक P और Q प्रतिच्छेद करते हैं। क्या PXQY एक आयत है? कारण दीजिए।
सिद्ध कीजिए कि, समांतर चतुर्भुज के चारों कोणों के समद्विभाजकों से बना चतुर्भुज आयत होता है।