Advertisements
Advertisements
Question
PQRS एक आयत है। S से PR पर डाला गया लंब ST कोण S को 2:3 के अनुपात में विभाजित करता है। ∠TPQ को ज्ञात कीजिए।
Solution
दिया गया है, ST ⊥ PR और ST, ∠S को 2:3 के अनुपात में विभाजित करते हैं।
इसलिए, अनुपात का योग = 2 + 3 = 5
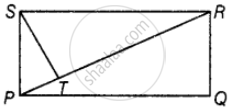
अब, `∠TSP = 2/5 xx 90^circ = 36°, ∠TSR = 3/5 xx 90^circ = 54°`
साथ ही, त्रिभुज के कोणों के योग के गुण से,
∠TPS = 180° – (∠STP + ∠TSP)
= 180° – (90° + 36°)
= 54°
हम जानते हैं कि, ∠SPQ = 90°
⇒ ∠TPS + TPQ = 90°
⇒ 54° + ∠TPQ = 90°
⇒ ∠TPQ = 90° – 54° = 36°
APPEARS IN
RELATED QUESTIONS
बताइए एक आयत उत्तल चतुर्भुज कैसे है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग को एक विशेष प्रकार का आयत समझा जा सकता है।
निम्न में से किस के लिए, सभी कोण बराबर होते हैं?
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
यदि किसी चतुर्भुज के विकर्ण बराबर हों तथा परस्पर समद्विभाजित करें, तो वह होता है एक ______।
यदि किसी समांतर चतुर्भुज के आसन्न कोण बराबर हों, तो वह है एक –
प्रत्येक समांतर चतुर्भुज एक आयत है।
प्रत्येक आयत एक समलंब है।
एक आयत ABCD में, AB = 25 cm और BC = 15 है। ∠C का समद्विभाजिक AB को किस अनुपात में विभाजित करता है?
नीचे दी गयी आक़ति में, एक आयत MORE दर्शाया गया है –
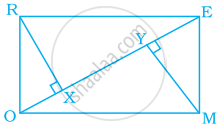
उचित कारण देते हुए, निम्न प्रश्नों के उत्तर दीजिए –
- क्या RE = OM है?
- क्या ∠MYO = ∠RXE है?
- क्या ∠MOY = ∠REX? है?
- क्या ∆MYO ≅ ∆RXE है?
- क्या MY = RX है?
