Advertisements
Advertisements
प्रश्न
Prove taht the points (-2 , 1) , (-1 , 4) and (0 , 3) are the vertices of a right - angled triangle.
उत्तर
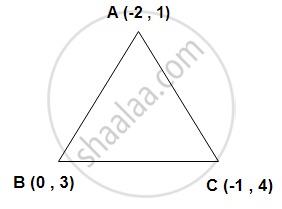
AB = `sqrt ((-2-0)^2 + (1-3)^2) = sqrt (4 + 4) = sqrt 8` units
BC = `sqrt ((10 + 1)^2 + (3 - 4)^2) = sqrt ( 1 + 1) = sqrt 2` units
AC = `sqrt ((-2 + 1)^2 + (1 - 4)^2) = sqrt (1 + 9) = sqrt 10` units
AB2+ BC2 = 8 + 2 = 10
AC2 = 10
∵ AB2+ BC2 = AC2
∴ A , B and C are the verices of a right angled triangle.
APPEARS IN
संबंधित प्रश्न
Find the values of y for which the distance between the points P (2, -3) and Q (10, y) is 10 units.
Find the centre of the circle passing through (6, -6), (3, -7) and (3, 3)
Using the distance formula, show that the given points are collinear:
(6, 9), (0, 1) and (-6, -7)
Show that the ▢PQRS formed by P(2, 1), Q(–1, 3), R(–5, –3) and S(–2, –5) is a rectangle.
Find the distance between the following pairs of points:
(-3, 6) and (2, -6)
A point P lies on the x-axis and another point Q lies on the y-axis.
Write the ordinate of point P.
Find the distance of the following points from origin.
(a+b, a-b)
Find the distance of the following points from origin.
(a cos θ, a sin θ).
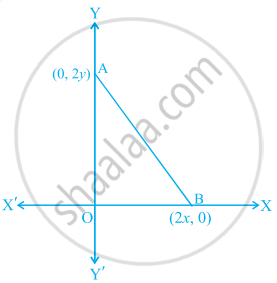
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
If the point A(2, – 4) is equidistant from P(3, 8) and Q(–10, y), find the values of y. Also find distance PQ.
