Advertisements
Advertisements
प्रश्न
पूर्णांकों के निम्नलिखित युग्म के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF × LCM है।
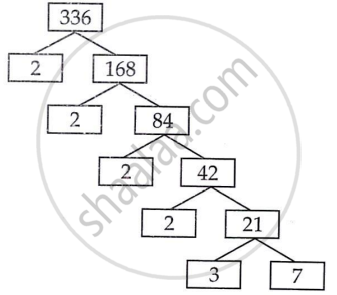
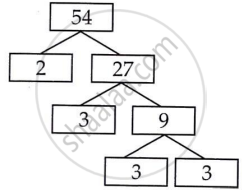
336 और 54
उत्तर
 |
 |
336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
336 और 54 का L.C.M = 2 × 3 × 3 × 3
336 और 54 का L.C.M = 3024
336 और 54 का H.C.F = 6
हम जानते हैं कि,
L.C.M × H.C.F = पहली संख्या × दूसरी संख्या
3024 × 6 = 336 × 26
18144 = 18144
इस प्रकार, LCM × HCF = दो संख्याओं का गुणनफल।
APPEARS IN
संबंधित प्रश्न
पूर्णांकों के निम्नलिखित युग्म के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF × LCM है।
26 और 91
पूर्णांकों के निम्नलिखित युग्म के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF × LCM है।
510 और 92
अभाज्य गुणनखंडन विधि द्वारा निम्नलिखित पूर्णांकों के HCF और LCM ज्ञात कीजिए:
12, 15 और 21
किसी पूर्णांक m के लिए, प्रत्येक सम पूर्णांक निम्नलिखित रूप का होता है
संख्या n2 – 1, 8 से विभाज्य होती है, यदि n है एक
वह सबसे बड़ी संख्या, जिससे 70 और 125 को विभाजित करने पर क्रमशः शेषफल 5 और 8 प्राप्त हों, है
यदि दो धनात्मक पूर्णांकों p और q को p = ab2 और q = a3b के रूप में व्यक्त किया जा सकता है, जहाँ a और b अभाज्य संख्याएँ हैं, तो LCM (p, q) है
1 से 10 तक की संख्याओं (दोनों सम्मिलित हैं) में से सभी संख्याओं से विभाज्य न्यूनतम संख्या है
क्या किन्हीं दो संख्याओं का HCF 18 और LCM 380 हो सकता है? कारण दीजिए।
दर्शाइए कि किसी प्राकृत संख्या n के लिए संख्या 12n अंक 0 या 5 पर समाप्त नहीं होगी।
