Advertisements
Advertisements
प्रश्न
पूर्णांकों के निम्नलिखित युग्म के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF × LCM है।
336 और 54
उत्तर
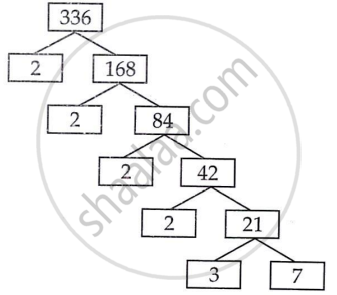 |
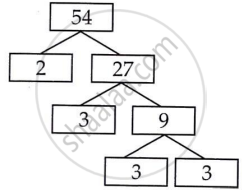 |
336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
336 और 54 का L.C.M = 2 × 3 × 3 × 3
336 और 54 का L.C.M = 3024
336 और 54 का H.C.F = 6
हम जानते हैं कि,
L.C.M × H.C.F = पहली संख्या × दूसरी संख्या
3024 × 6 = 336 × 26
18144 = 18144
इस प्रकार, LCM × HCF = दो संख्याओं का गुणनफल।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित संख्या को अभाज्य गुणनखंड के गुणनफल के रूप में व्यक्त कीजिए:
140
अभाज्य गुणनखंडन विधि द्वारा निम्नलिखित पूर्णांकों के HCF और LCM ज्ञात कीजिए:
12, 15 और 21
व्याख्या कीजिए कि 7 × 11 × 13 + 13 और 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्याएँ क्यों हैं।
किसी पूर्णांक m के लिए, प्रत्येक सम पूर्णांक निम्नलिखित रूप का होता है
यदि 65 और 117 के HCF को 65m – 117 के रूप में व्यक्त किया जा सके तो m का मान है
वह सबसे बड़ी संख्या, जिससे 70 और 125 को विभाजित करने पर क्रमशः शेषफल 5 और 8 प्राप्त हों, है
यदि दो धनात्मक पूर्णांकों a और b को a = x3y2 और b =xy3 के रूप में व्यक्त किया जाए, जहाँ x और y अभाज्य संख्याएँ हैं, तो HCF (a, b) है
यदि दो धनात्मक पूर्णांकों p और q को p = ab2 और q = a3b के रूप में व्यक्त किया जा सकता है, जहाँ a और b अभाज्य संख्याएँ हैं, तो LCM (p, q) है
1 से 10 तक की संख्याओं (दोनों सम्मिलित हैं) में से सभी संख्याओं से विभाज्य न्यूनतम संख्या है
दर्शाइए कि किसी प्राकृत संख्या n के लिए संख्या 12n अंक 0 या 5 पर समाप्त नहीं होगी।
