Question

R त्रिज्या वाली समांग डिस्क से R/2 त्रिज्या का एक वृत्ताकार भाग काट कर निकाल दिया गया है। इस प्रकार बने वृत्ताकार सुराख का केन्द्र मूल डिस्क के केन्द्र से R/2 दूरी पर है। अवशिष्ट डिस्क के गुरुत्व केन्द्र की स्थिति ज्ञात कीजिए।

Answer 1

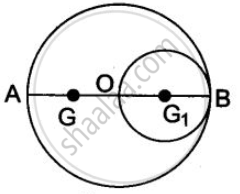
माना दिए हुए वृत्ताकार पटल का केन्द्र O और व्यास AB है।
OA = OB = R = त्रिज्या
इस पटल से, व्यास OB को एक वृत्त काट कर निकाल दिया जाता है।
स्पष्टत: दिए हुए पटल का गुरुत्व केन्द्र O पर तथा काटे गए वृत्त का गुरुत्व केन्द्र उसके केन्द्र G₁ पर होगा, जबकि
OG₁ = `1/2 . "OB" = 1/2 "R"`

∵ वृत्तों के क्षेत्रफल उनकी त्रिज्याओं के वर्गों के अनुपात में होते हैं।

∴ `"काटे गए वृत्त का क्षेत्रफल"/"पूरे पटल का क्षेत्रफल" = ((1/2"R")^2)/"R"^2 = ((1/4"R")^2)/"R"^2 = 1/4`

अर्थात  `"काटे गए वृत्त का क्षेत्रफल" = 1/4 ("पूरे पटल का क्षेत्रफल")`

माना पूरे पटल का भार 4W है, तब कटे हुए वृत्त का भार W हुआ।

∴ शेष पटल का भार  = 4W - W = 3W

यदि शेष भाग का गुरुत्व केन्द्र G है जो स्पष्टतया व्यास AB पर होगा, तब बिन्दु O के परितः आघूर्ण लेने पर,

`3 "W" . "OG" = "W" . "OG"_1` या `"OG" = 1/3  "OG"_1 = 1/3  .  1/2  "R" = 1/6  "R"`

अतः पटल के केन्द्र से शेष भाग के गुरुत्व केन्द्र की दूरी `"R"/6` है।