Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
उत्तर
(a)
(b)
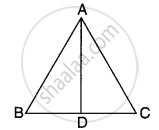
मान लीजिए कि दो समरूप ∆ABC ∼ ∆PQR हैं, जिनकी संगत माध्यिकाएँ AD एवं PM हैं। (देखिए आकृति)
चूँकि ∆ABC ∼ ∆PQR दिया है।
∠A = ∠P, ∠B = ∠Q
एवं ∠C = ∠R …(1)
एवं `"AB"/"PQ" = "BC"/"QR" = "CA"/"RP"` …(2) [समरूप त्रिभुजों के प्रगुण]
∵ `"AB"/"PQ" = "BC"/"QR" = (2"BD")/(2"QM") = "BD"/"QM"` ….(3)
[D, BC का एवं M, QR का मध्य-बिन्दु है]
अब ∆ABD एवं ∆PQM में,
∠B = ∠Q [समीकरण (1) से]
एवं `"AB"/"PQ" = "BD"/"QM"` ........[समीकरण (3) से]
⇒ ∆ABD ∼ ∆PQM .........[SAS समरूपता]
⇒ `"AB"/"PQ" = "AD"/"PM"` ............(4) [समरूप त्रिभुजों के प्रगुण]
अब ∵ `("ar"("ABC"))/("ar"("PQR")) = ("AB"/"PQ")^2` ............ (5) [समरूप त्रिभुजों का क्षेत्रफल प्रगुण]
⇒ `("ar"("ABC"))/("ar"("PQR")) = ("AD"/"PM")^2` ........[समीकरण (4) एवं (5) से]
अतः दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
इति सिद्धम्
APPEARS IN
संबंधित प्रश्न
मान लीजिए ∆ABC ∼ ∆DEF है और इनके क्षेत्रफल क्रमश: 64 cm2 और 121 cm2 हैं। यदि EF = 15.4 cm हो, तो BC ज्ञात कीजिए।
एक समलंब ABCD जिसमें AB || DC है, के विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि AB = 2CD हो तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को O पर प्रतिच्छेद करे, तो दर्शाइए कि `("ar"("ABC"))/("ar"("DBC")) = "AO"/"DO"` हैं।
यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
एक त्रिभुज ABC की भुजाओं AB, BC और CA के मध्य-बिंदु क्रमश: D, E और F हैं। ∆DEF और ∆ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है: ______
दो समरूप त्रिभुजों की भुजाएँ 4 : 9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात है: _____
सिद्ध कीजिए कि एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
PQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM ⊥ QR है। दर्शाइए कि PM² = QM.MR है।
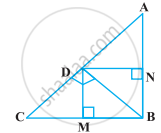
आकृति में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD ⊥ AC तथा DM ⊥ BC और DN ⊥ AB है। सिद्ध कीजिए कि
(i) DM2 = DN.MC
(ii) DN2 = DM.AN